Question

Draw the graph of the relation $y^2(x-1)=x^2(1+x)$

Explanation

We have `y^(2)(x-1)=x^(2)(1+x)`
or `y=+-xsqrt(x+1)/(x-1)`
Let us first draw the graph of `y=f(x)=xsqrt((x+1)/(x-1))`
Clearly,the domain of the function is `(-infty, -1) cup (1, infty)`
`f(x)=0 therefore x=0,1`
So the graph meets the x-axis at (0,0) and `(-1,0)`.
Also, `f(x) ge0` for `x ge1` and `f(x) lt 0` for `x lt -1`
`f^(')(x) =1.sqrt((x+1)/(x-1))+x((x-1-(x+1))/(x-1)^(2))/(2sqrt((x+1)/(x-1))`
`=(x^(2)-x-1)/((x-1)^(2)sqrt(x+1)/(x-1))`
`=((x-1(1-sqrt(5))/(2))(x-(1+sqrt(5))/2))/((x-1)^(2)sqrt((x+1)/(x-1)))`
`f^(')(x)=0 therefore x=(1+sqrt(5))/(2)`, which is the point of minima.
`x=(1-sqrt(5))/(2)` is not a critical point as `-1 lt (1-sqrt(5))/(2) lt 1`
`f(x)` decreases for `(-infty, -1) cup (1, (1+sqrt(5))/(2))`
`f(x)` increases for `(1+sqrt(5))/(2), infty`
Also `underset(x to 1^(+))xsqrt((x+1)/(x-1))=infty`
So the graph of `y=f(x)=xsqrt((x+1)/(x-1))` is as shown in the following figure.

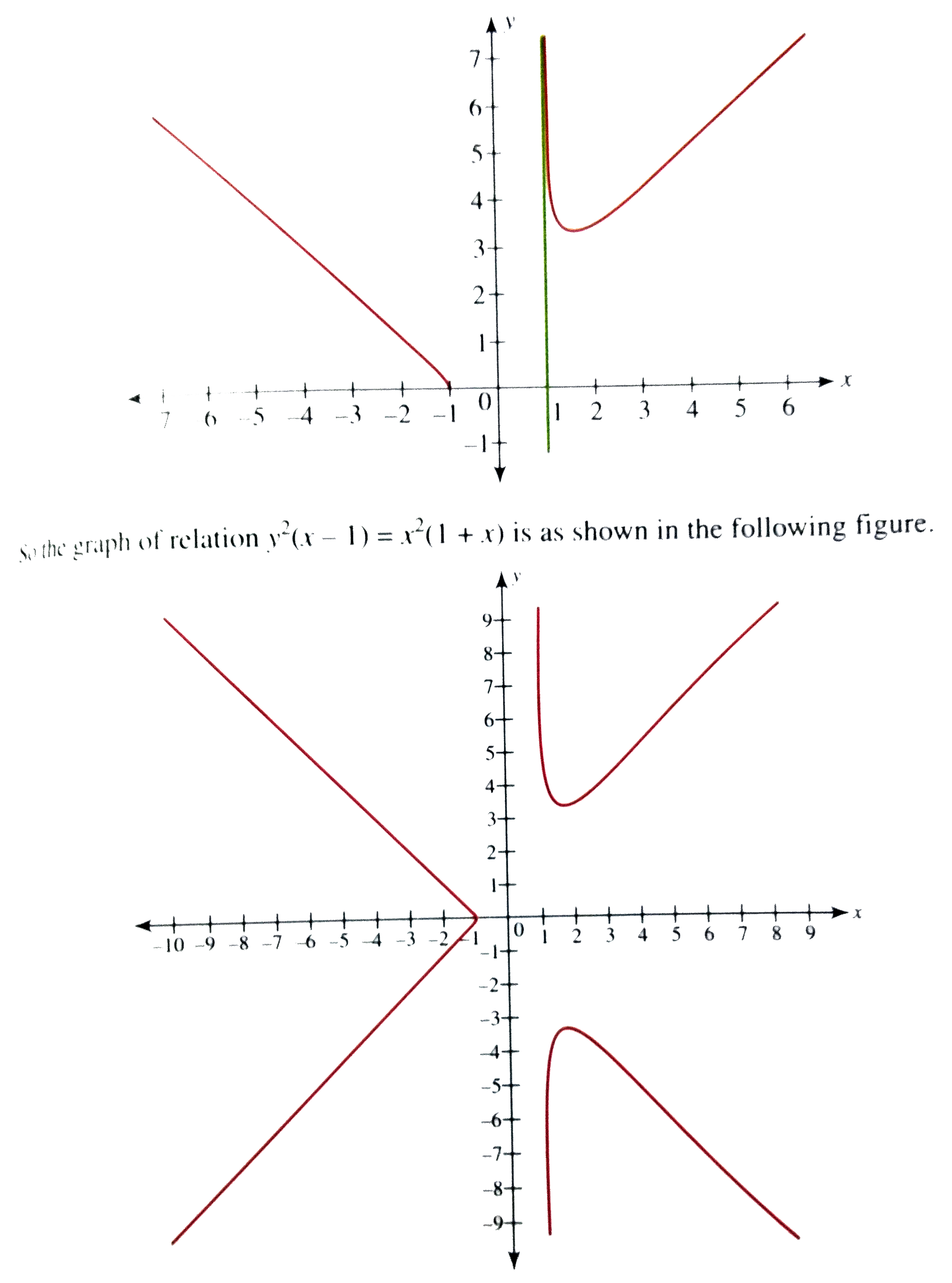
So the graph of relation `y^(2)(x-1)=x^(2)(1+x)` is as shown in the following figure.