Two discs A and B of radii 'R' and '2R' respectively are placed on a horizontal surface as shown. Keeping the disc A motionless, disc B is rotated around it without slippage. When the disc B returns to its startin position, the angle that it has turned is equal to :

3π radians
2π radians
6π radians
π radians
The correct Answer is:A
VC=ω1×3R
VPC=3ω1R−ω2×2R=0
3ω1=2ω2
3x2πt=2θt
θ=3π

Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Physics, SECTION-1 (PART-A) [COMPREHENSION TYPE]
2 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Physics, SECTION-1 (PART-A) [MULTIPLE CORRECT CHOICE TYPE]
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS
60 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
If two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
View Solution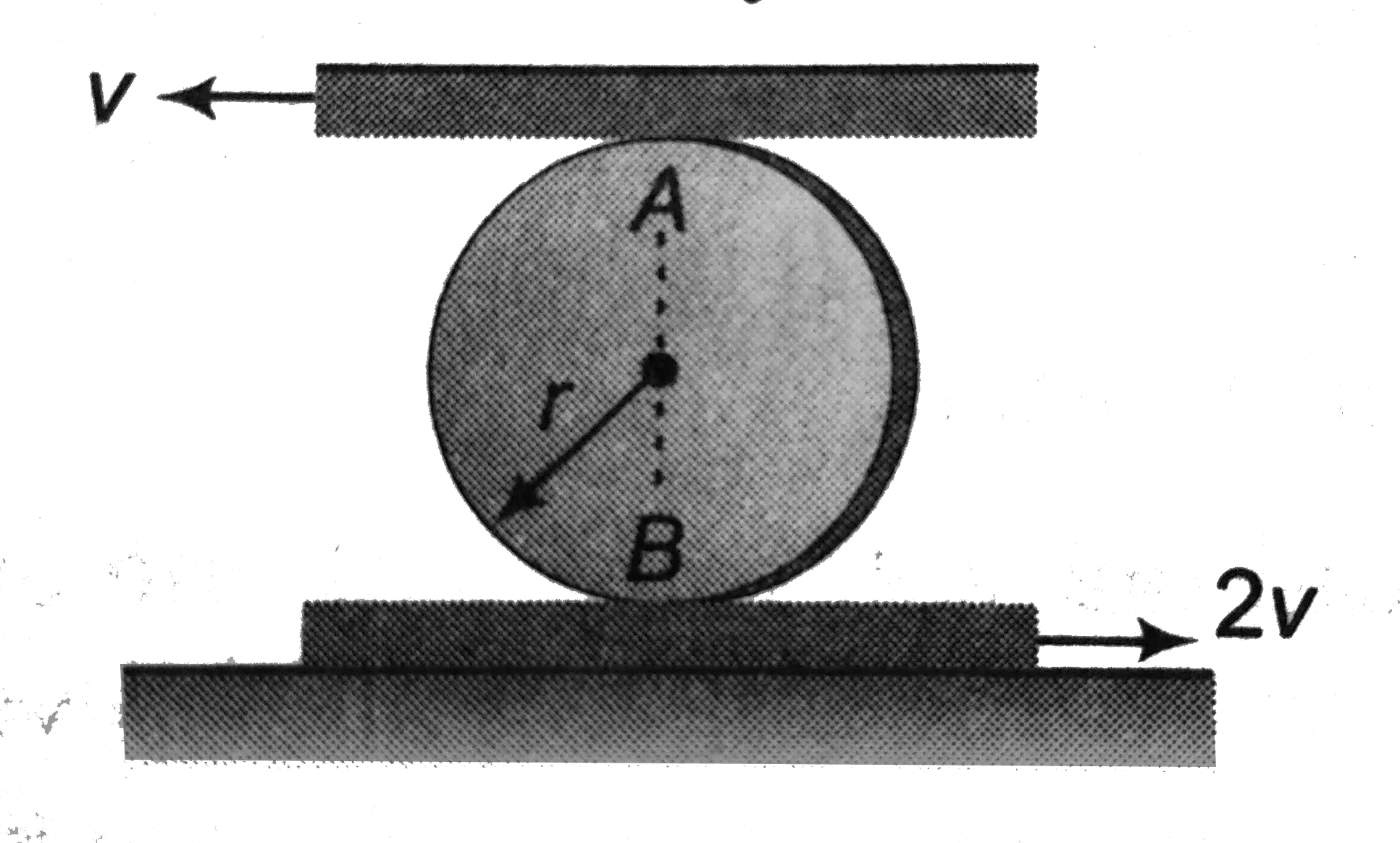
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View Solution
Knowledge Check
If two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
Athe same as that of BBtwice that of BCfour times that of BDone-fourth that of BA disc of a mass M and radius R can rotate freely in vertical plane about a horizontal axis at O. Distant r from the centre of disc as shown in the figure. The disc is released from rest in the shown position.

The angular acceleration of disc when OC rotates by an angles of 37∘ isA8rg5[R2+2r2]B5rg4[R2+2r2]C10rg3[R2+2r2]D8rg5R2A disc of mass m and radius r placed on a routh horizontal surface. A cue of mass m hits the disc at a height h from the axis passing through centre and parallel to the surface. The disc will start pure rolling for.
Ah<r3Bh=r2Ch>r2Dh≥r2

the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
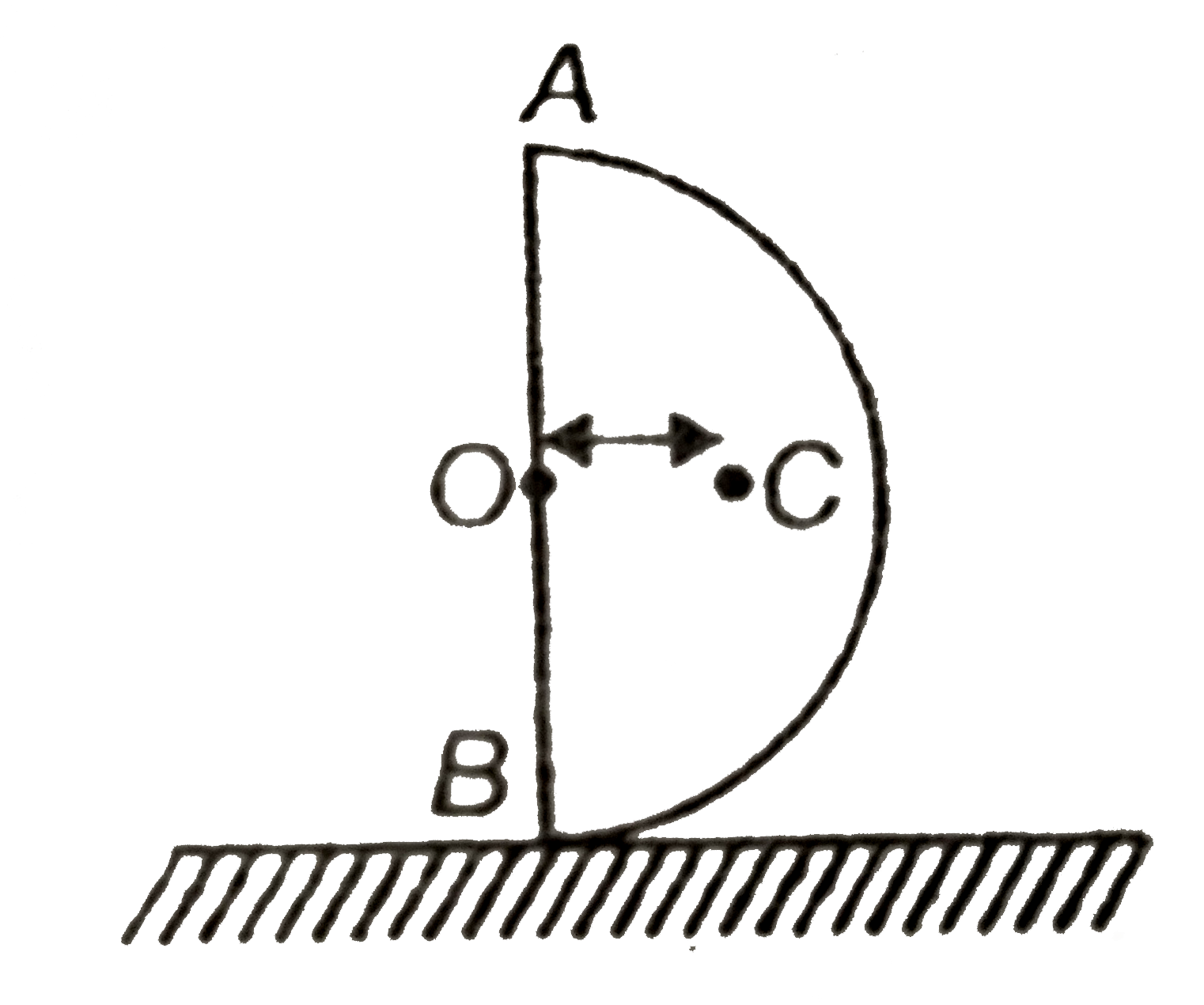
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find

(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View SolutionA coin placed on a horizontal rotating disc, with its centre at 10 cm from the centre of the disc, is about to slip off when the disc performs 60 rpm. Find the coefficient of friction between the coin and the disc.
View SolutionA disc of a mass M and radius R can rotate freely in vertical plane about a horizontal axis at O. Distant r from the center of disc as shown in the figure. The disc is released from rest in the shown position.

The angular acceleration of disc when OC rotates by an angles of 37∘ is
View Solution
