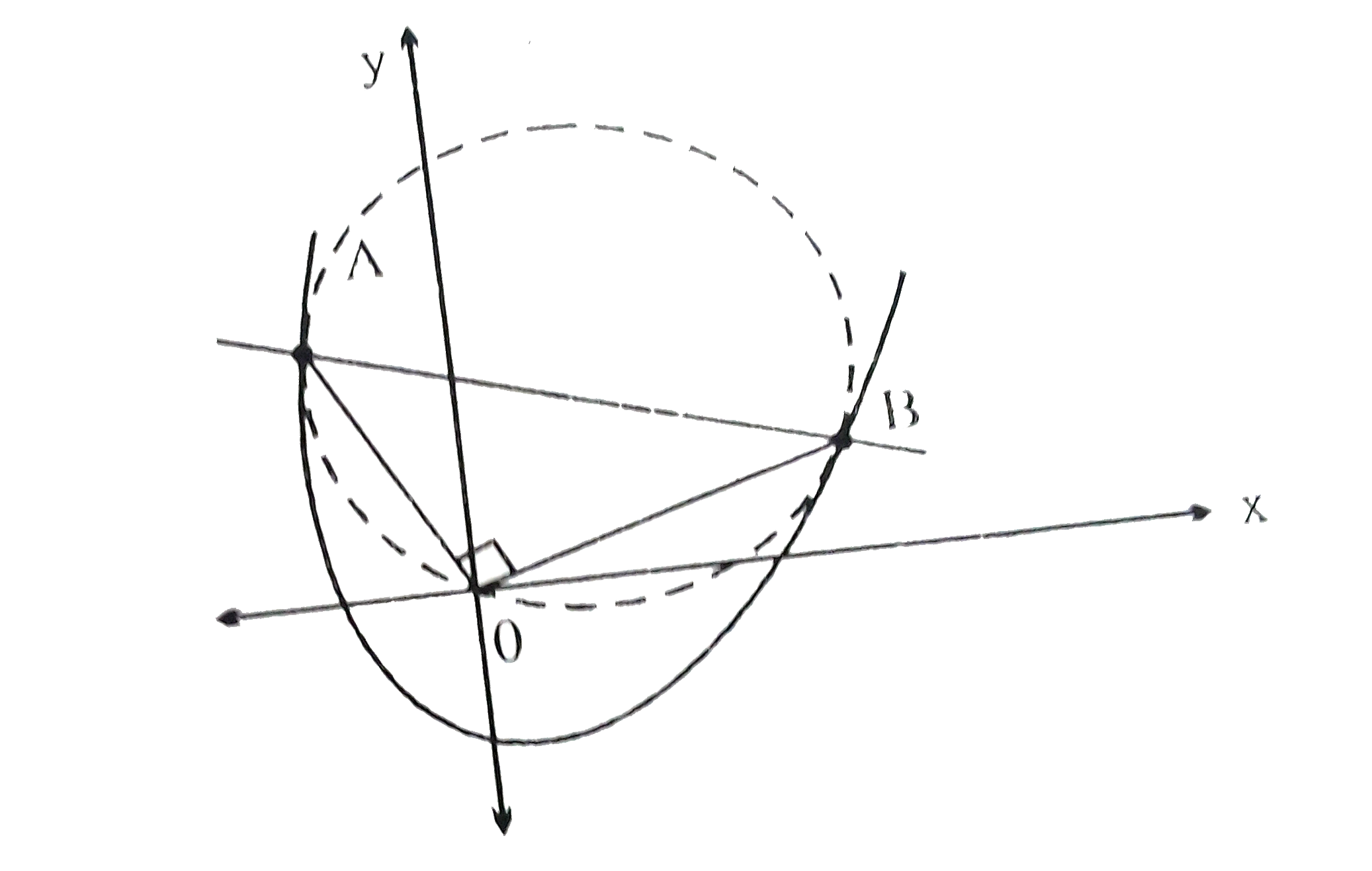
The line (a−1)x+ay=1 intersects the curve 3x2+4xy+2y2=1 at points A and B. The circle on AB as diameter passes through the origin, then find the sum of all possible value of 'a'.
Homogenise the given curve with given line.
3x2+4xy+2y2−((a−1)x+ay)2=0
Coeff. of x2+Coeff. of y2=0
3+2−(a−1)2−a2=0
5−a2−1+2a−a2=0
2a2−2a−4=0
a2−a−2=0
Sum of roots =1
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION-1 Part-A (Single Correct choice Type )
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION-1 Part-A (Comprehension type )
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Chemistry, SECTION-2 (PART-C)
10 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View SolutionLine 3x+by=k intersect the curve 2x2+3y2+2xy=1 at points A and B. Thecircle on AB as diameter passes through origin,then sum of all possible values of 'k' is
View SolutionLine 3x+6y=k intersect the curve 2x2+3y2+2xy=1 at points A and B. Thecircle on AB as diameter passes through origin,then sum of all possible values of 'k' is
View SolutionThe line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View SolutionSuppose the ine x+2y=k intersects the conic 2x2+5xy+3y2=1 in two points A and B. If the circle with AB as diameter passes through the origin, then value of 14k2 is
View SolutionLine x+ ay =1 cuts the circle x2+y2−4x−2y+1=0 at two points A and B such that Chord AB subtends an angle of 90∘ at origin then sum of possible values of a is
View SolutionLine x+ ay =1 cuts the circle x2+y2−4x−2y+1=0 at two points A and B such that Chord AB subtends an angle of 90∘ at origin then sum of possible values of a is
View SolutionLine x+ay=1 cuts the circle x2+y2−4x−2y+1=0 at two points A and B such that Chord AB subtends an angle of 90∘ at origin then sum of possible values of α is
View SolutionIf the straight line represented by x cos α + y sin α = p intersect the circle x2+y2=a2 at the points A and B , then show that the equation of the circle with AB as diameter is (x2+y2−a2)−2p(xcosα+ysinα−p)=0
View SolutionFor the curve y=4x3−2x5,find all the points at which the tangent passes through the origin
View Solution
