Suppose the line, $L_{1}$ has equation $10 x - 12 y = - 17 . The line L_{2} intersect L_{1} at (\frac{1}{2}, \frac{11}{6})$
and is perpendicular to $L_{1} .$ Find the abscissa of the point on $L_{2}$ whose ordinate is (1)/(30).

Video Solution

Text Solution

Verified by Experts

Equation of $L_{2}, y - \frac{11}{6} = \frac{- 6}{5} (x - \frac{1}{2})$
if $y = \frac{1}{30}, \frac{1}{30} - \frac{11}{6} = \frac{- 6 x}{5} + \frac{3}{5}$
$\frac{1}{6} - \frac{55}{6} - 3 = - 6 x$
$6 x = 3 + \frac{54}{6} = 12$
$x = 2$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

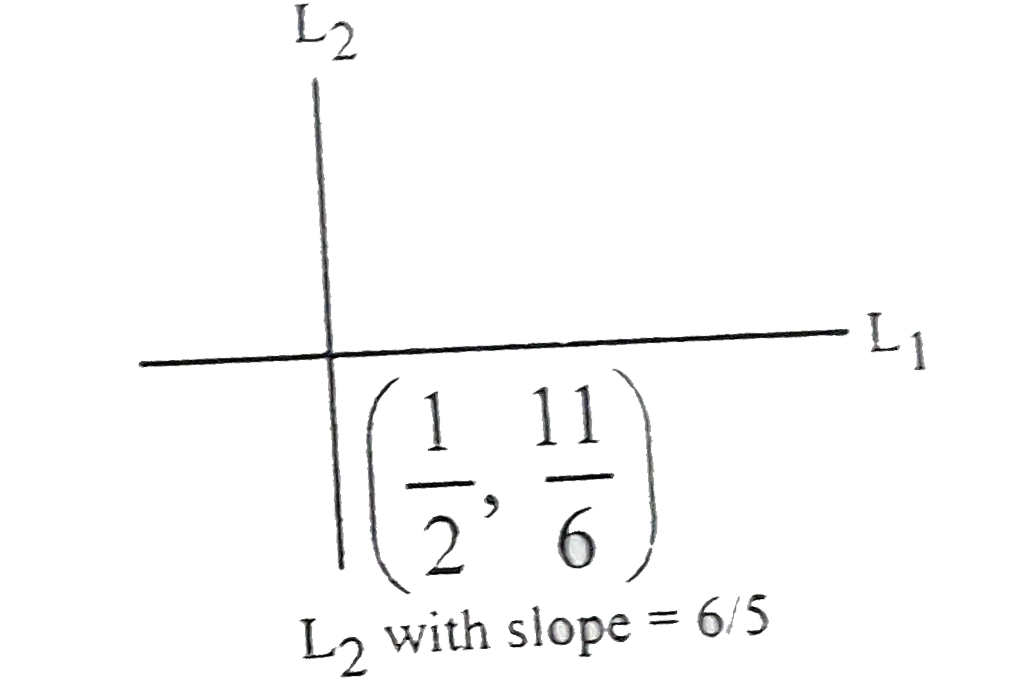
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Suppose that the points $(h, k)$ , $(1, 2)$ and $(- 3, 4)$ lie on the line $L_{1}$ . If a line $L_{2}$ passing through the points $(h, k)$ and $(4, 3)$ is perpendicular to $L_{1}$ , then $k / h$ equals
A $- \frac{1}{7}$
B $\frac{1}{3}$
C $3$
D $0$
Question 2 - Select One
A line L passeds through the points $(1, 1) and (2, 0)$ and another line L' passes through $(\frac{1}{2}, 0)$ and perpendicular to L. Then the area of the triangle formed by the lines L, L' and Y-axis is
A $\frac{15}{8}$
B $\frac{25}{4}$
C $\frac{25}{8}$
D $\frac{25}{16}$
Question 3 - Select One
If points $(h, k) (1, 2)$ and $(- 3, 4)$ lie on line $L_{1}$ and points $(h, k)$ and $(4, 3)$ lie on $L_{2}$ . If $L_{2}$ is perpendicular to $L_{1}$ , then value of $\frac{h}{k}$ is
A $- \frac{1}{7}$
B $\frac{1}{3}$
C3
D7

BANSAL-TEST PAPERS-Mathematics, SECTION-3 (PART-C)

Home
Ask Doubt
Profile