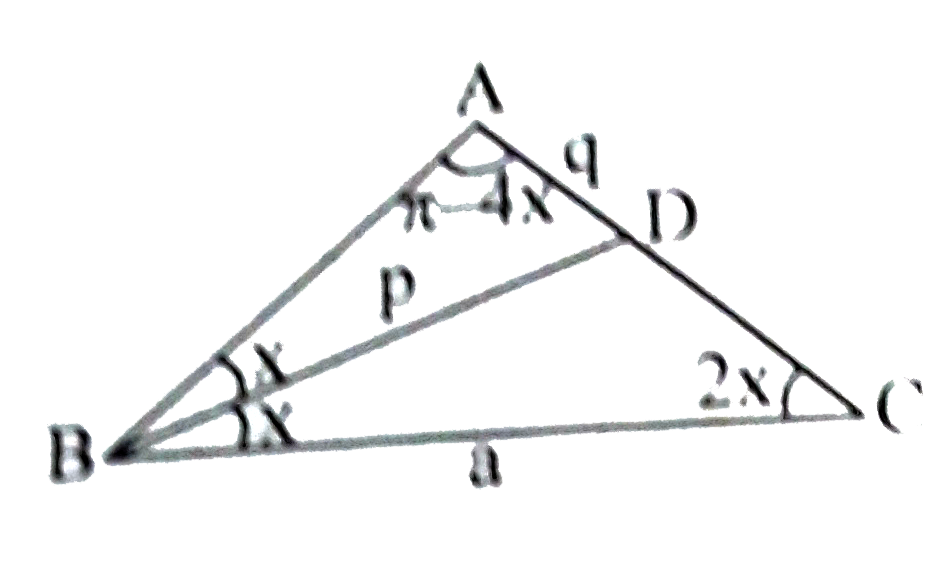
Let triangle ABC be an isosceles triangle with AB=AC. Suppose that the angle bisector of its angle B meets the side AC at a point D and that BC=BD+AD. Find angle A (in degrees).
BC=BD+AD
a=p+q
or ap=1+qp
using Sine law in ΔABD
sin3xsin2x=1+sinxsin4x⇒sin3x.sin4x−sinx.sin2xsin2x.sin4x=1
2sin3x.sin4x−2sinx.sin2x=2sin2x.sin4x
(cosx−cos7x)−(cosx−cos3x)=cos2x−cos6x
cos3x−cos7x=cos2x−cos6x
2sin5x.sin2x=2sin4x.sin2x
as sin5x=sin4x
5x+4x=180∘ ⇒ x=20∘, hence ∠A=180∘−80∘=100∘
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION-1 Part-A (Single Correct choice Type )
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION-1 Part-A (Comprehension type )
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Chemistry, SECTION-2 (PART-C)
10 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Video
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
Let triangle ABC be an isosceles with AB=AC. Suppose that the angle bisector of its angle B meets the side AC at a point D and that BC=BD+AD. Measure of the angle A in degrees, is :
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View Solution
Knowledge Check
Let triangle ABC be an isosceles with AB=AC. Suppose that the angle bisector of its angle B meets the side AC at a point D and that BC=BD+AD. Measure of the angle A in degrees, is :
A80B100C110D130ΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
A60∘B90∘C120∘Dcan't be determinedIn the triangle ABC, the internal bisector of angle A meets the side BC at D. If BD=7.5 cm and BC=9 cm. Then calculate the value of AB:AC.
A2 :1B1 :2C5 :1D1 :3
ABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View SolutionIn a ΔABC,∠C in an obtuse angle . The bisectors of the exterior angles at A and B meet BC and AC produced at D and A respectively . If AB=AD=BE. Find ∠ACB .
View SolutionIn △ABC, AD is the internal bisector of ∠S, meeting the side BC at D. If BD = 5cm, BC = 7.5 cm, then AB:AC is:
View SolutionIn an isosceles triangle ABC, AB=AC and ∠A=3∠B. Find ∠C.
View SolutionIn a △ABC. AB = 5 cm, AC = 7 cm. If AD is the angle bisector of angle A, then BD :CD is :
View Solution
