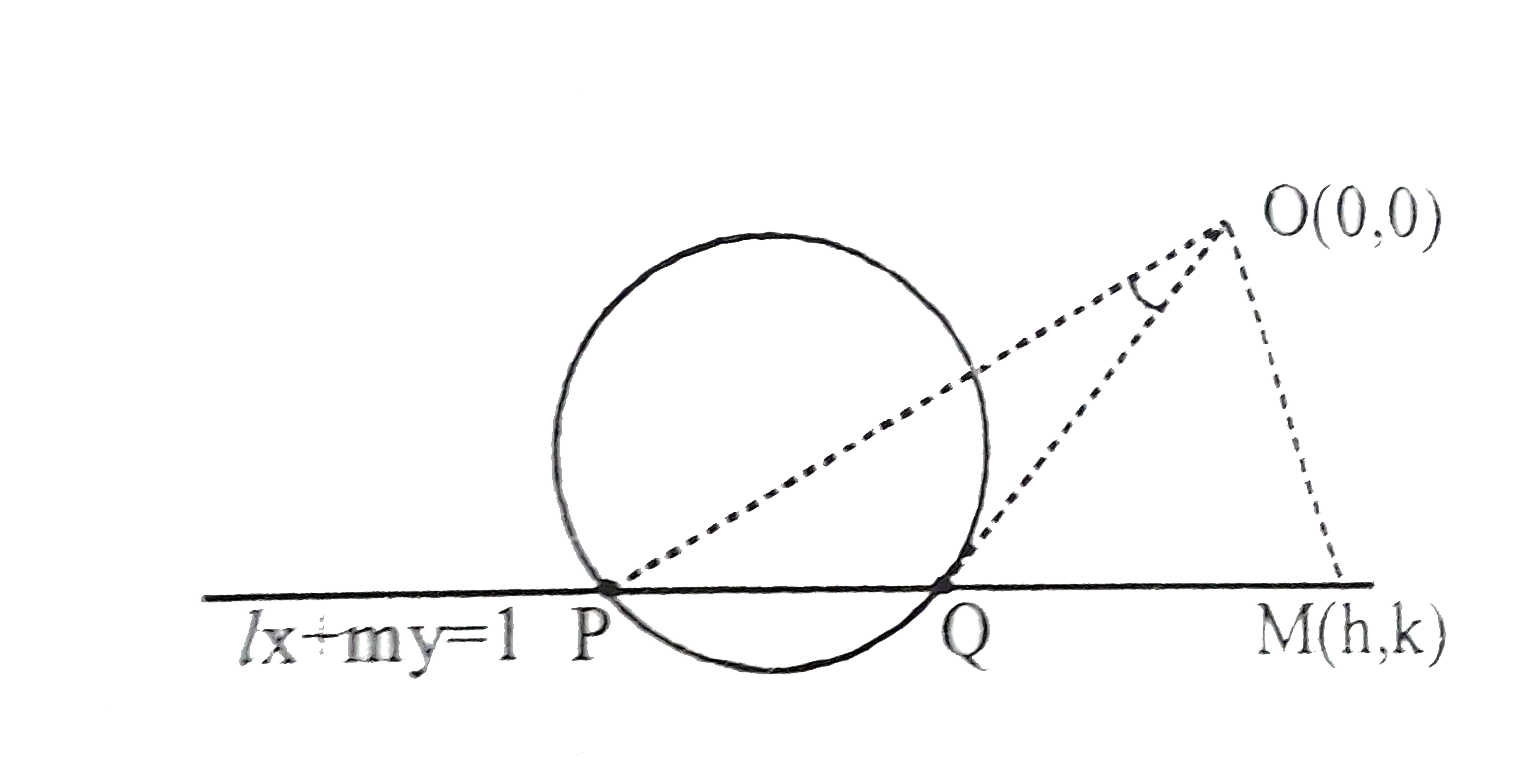
A variable line lx+my=1 (where l and m are parameters) intersect a circle x2+y2−4x+3=0 at the points P and Q. The chord PQ subtends a right angle at the origin. If the locus of foot of perpendicular drawn from origin on the given variable lines is λx2+μy2−4x+3=0, then find the value of (λ+μ).
Homogenising circle with variable line
x2+y2−4x(lx+my)+3(lx+my)2=0
Since OP and OQ are at right angle.
∴Coefficient of x2+coeff. Of y2=0
(1−4l+3l2)+(1+3m2)=0
3l2+3m2−4l+2=0 …(1)
Let foot of perpendicular is (h,k)
∴ lh+mk=1 ...(2)
Equation of OM is y=mlx
mh=lk ...(3)
From (2) and (3) we get l=hh2+k2 and m=kh2+k2
l2+m2=1h2+k2 using this in (1)
3h2+k2−4hh2+k2+2=0
∴ Required locus is 2x2+2y2−4x+3=0
∴ λ=μ=2
∴ λ+μ=4
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION-1 Part-A (Single Correct choice Type )
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION-1 Part-A (Comprehension type )
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Chemistry, SECTION-2 (PART-C)
10 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
A variable line cuts pair of lines x2−(a+b)x+ab=0 in such a way that intercept between subtends a right angle at origin. The locus of the foot of the perpendicular from origin on variable line is
View SolutionThe locus of foot of the perpendicular drawn from a fixed point (2,3) to the variable line y=mx, m being variable is
View SolutionThe locus of the foot of the perpendicular drawn from origin to a variable line passing through fixed point (2,3) is a circle whose diameter is
View SolutionThe locus of the foot of perpendicular drawn from origin to a variable line passing through fixed points (2,3) is a circle whose diameter is?
View SolutionThe locus of the midpoint of the chord of the circle x2+y2=4 which subtends a right angle at the origin is?
View SolutionThe locus of the mid-points of a chord of the circle x2+y2=4 which subtends a right angle at the origin is
View SolutionLine x+ ay =1 cuts the circle x2+y2−4x−2y+1=0 at two points A and B such that Chord AB subtends an angle of 90∘ at origin then sum of possible values of a is
View SolutionLine x+ ay =1 cuts the circle x2+y2−4x−2y+1=0 at two points A and B such that Chord AB subtends an angle of 90∘ at origin then sum of possible values of a is
View SolutionThe locus of the mid point of a chord of the circle x2+y2=4 which subtends a right angle at the origin is
View SolutionThe locus of the foot of the perpendicular, from the origin to chords of the circle x2+y2−4x−6y−3=0 which subtend a right angle at the origin, is:
View Solution
