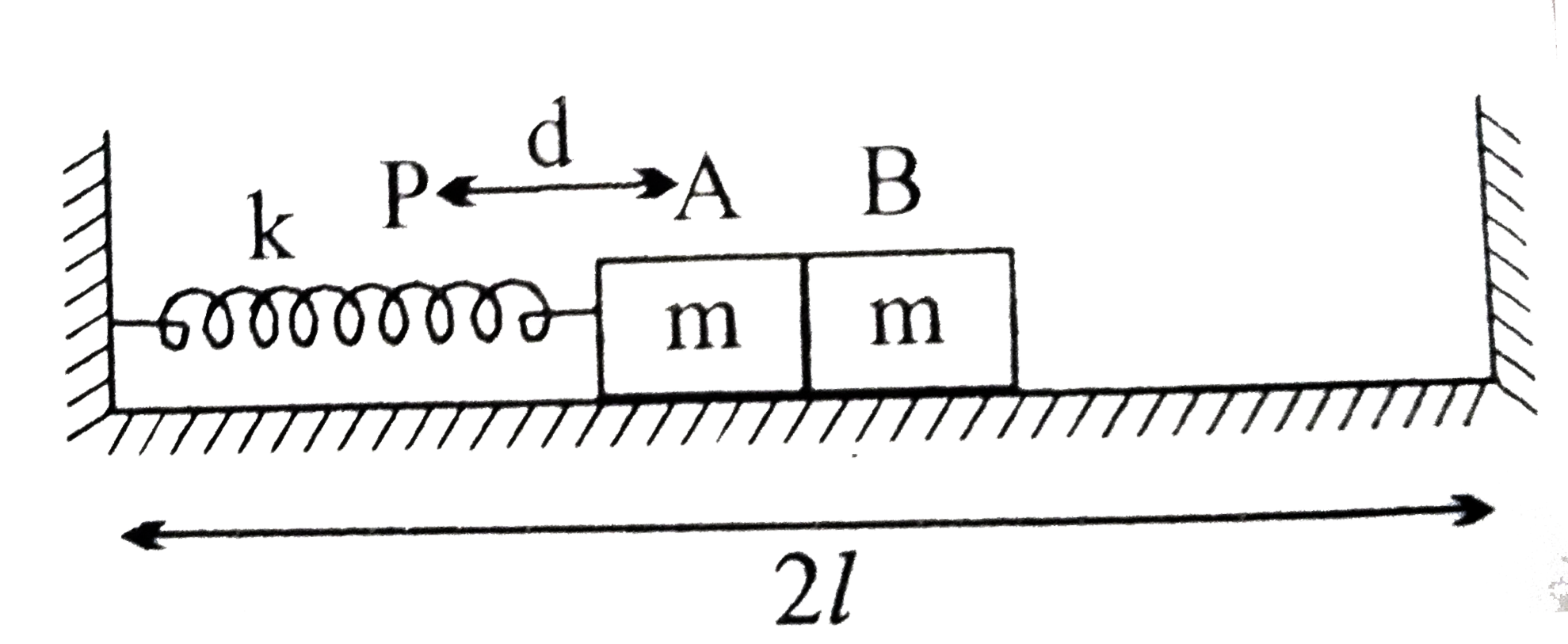
Two small blocks A and B of sam mass m are placed at the mid point of a smooth horizontal track of length 2l as shown. A massless spring of force constant k and free length l is touching the block A but is not attached to it. The block A is displaced towards left by a small distance d=AP thereby causing a compression in the spring. The block is then let free to move. The minimum time after colliding with B the block A again reaches its starting position is "πT" milli second. Find 'T' (Assume elastic collision )
Take m=1k and K=100N/m, l=πcm, d=1 cm.
0300
VA max=Aω=d√Km=VB
∴ time taken to reach its initial position by 'A' =π√mk+2lV=π√mk+2ld√mK
=√11000[π+2×x1]
πT×10−3=3π10sec.
T=300
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY SECTION-2 Part-C ( Integer type )
10 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 Part-C[ Integer type ]
10 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 Part-B[ Matrix type ]
2 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
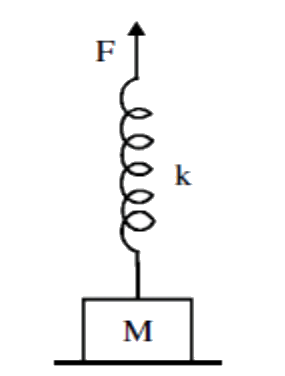
A block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is
 AkL22MB√MkL(c)SCML2kDzero
AkL22MB√MkL(c)SCML2kDzeroTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBv√v2kC√mvkDmv2k
The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionA block A of mass M is placed in contact with a fixed spring of length l and force constant k and free from a smooth wall at a distance l on the other side. If the block is given a velocity v as shown, the time taken by the block to strike on the wall will be

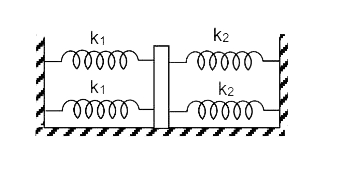
View SolutionA block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
View Solution
