A horizontal pipe of cross-sectional area is joined to a lower pipe of cross-sectional area . The entire pipe is full of liquid with density , and the left end is at atmospheric pressure . A small open tube extends upwards from the lower pipe is closed , . Find k
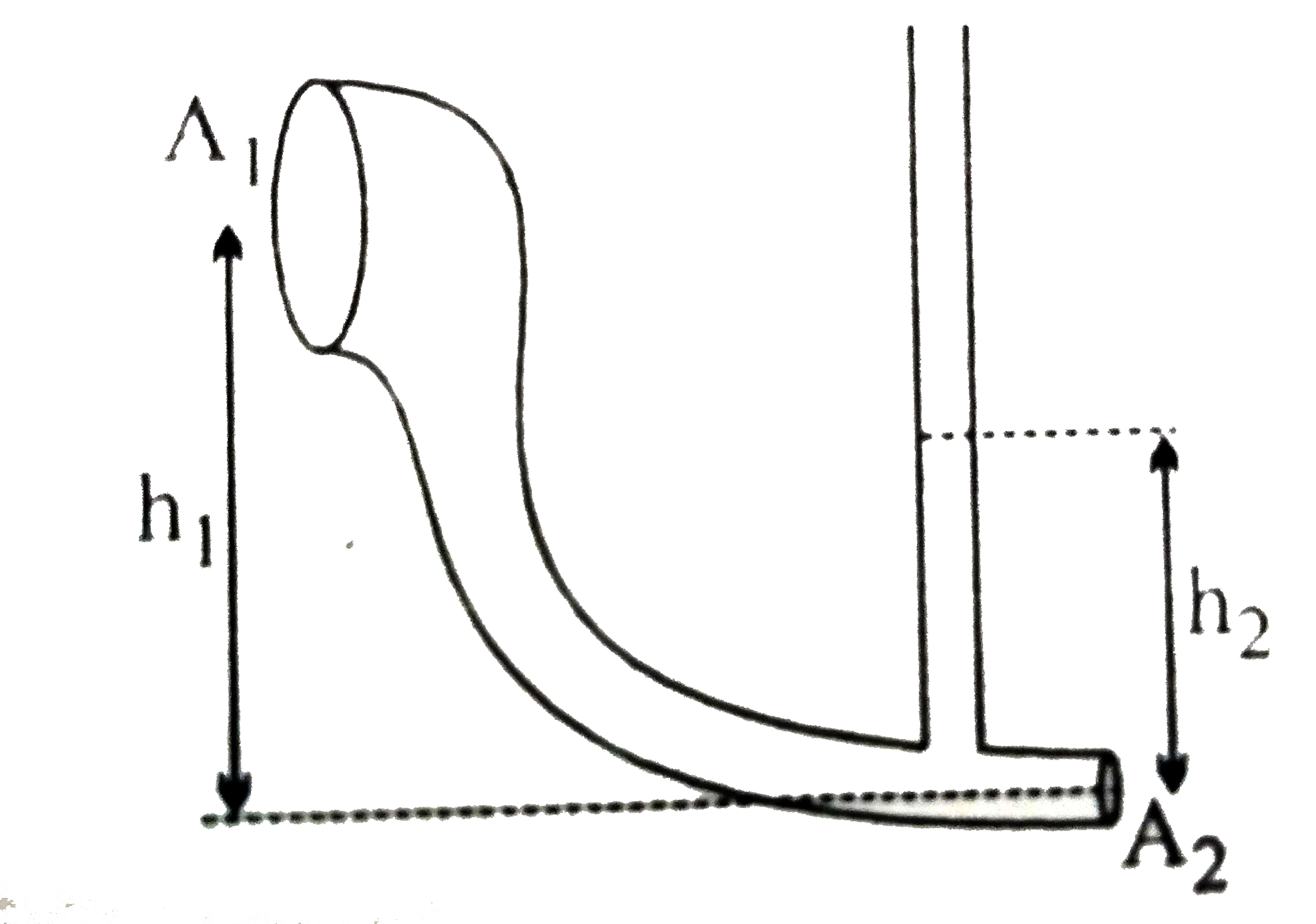
(i) When right end is closed
Applying Bernoulli's equation along a stream line at 1 & 2
……(1)
Also ……(2)
Thus from equation (1) & (2) we get
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY SECTION-2 Part-C ( Integer type )
10 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 Part-C[ Integer type ]
10 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 Part-B[ Matrix type ]
2 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
A lawn sprinkler has 20 holes, each of cross-sectional area 2.0x10−2cm2, and is connected to a hose pipe of cross sectional area 2.4cm2. If the speed of water in the hose pipe is 1.5ms−1, the speed of water as it emerges from the holes is
View SolutionFresh water flows horizontally from pipe section 1 of cross-sectional area A, into pipe section 2 of cross-sectional area A2 Figure gives a plot of the pressure difference p2−p1 versus the inverse area squared A−21 that would be expected for a volume flow rate of a certain value if the water flow were laminar under all circumstances. The scale on the vertical axis is set by Δps=600kN/m2. For the conditions of the figure, what are the values of (a) A2 and (b) the volume flow rate?
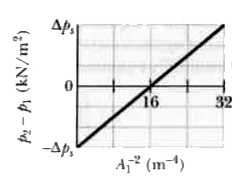
View Solution
Knowledge Check
A lawn sprinkler has 20 holes, each of cross-sectional area 2.0x10−2cm2, and is connected to a hose pipe of cross sectional area 2.4cm2. If the speed of water in the hose pipe is 1.5ms−1, the speed of water as it emerges from the holes is
A2.25ms−1B4.5ms−1C9ms−1D18ms−1A liquid flows through a pipe of non-uniform cross-section. If A1andA2 are the cross-sectional areas of the pipe at two points, the ratio of velocities of the liquid at these points will be
AA1A2BA1A2CA2A1D1A1A2From a horizontal tube with area of cross-section A1 and A2 as shosn in fiugre liquid is flowing in the level of the liauid in the two veritcal tunes is h.
 AThe volume of the liquid flowing through the tube in time is A1v1Bv2−v1=√2ghCv22−v11=2ghDThe energy per unit mass of the liquid is the same in both sections of the tube
AThe volume of the liquid flowing through the tube in time is A1v1Bv2−v1=√2ghCv22−v11=2ghDThe energy per unit mass of the liquid is the same in both sections of the tube
A container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
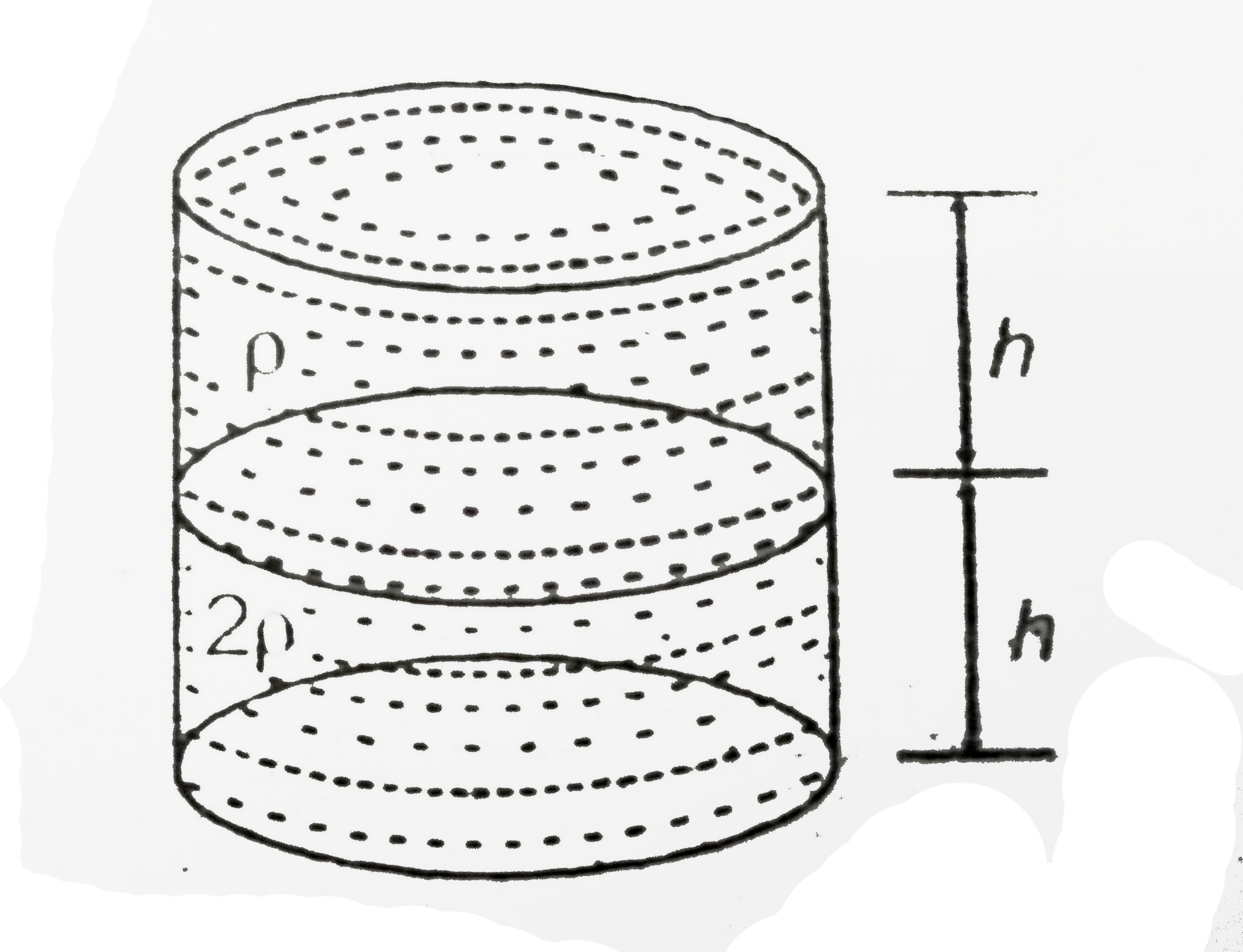
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is

View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
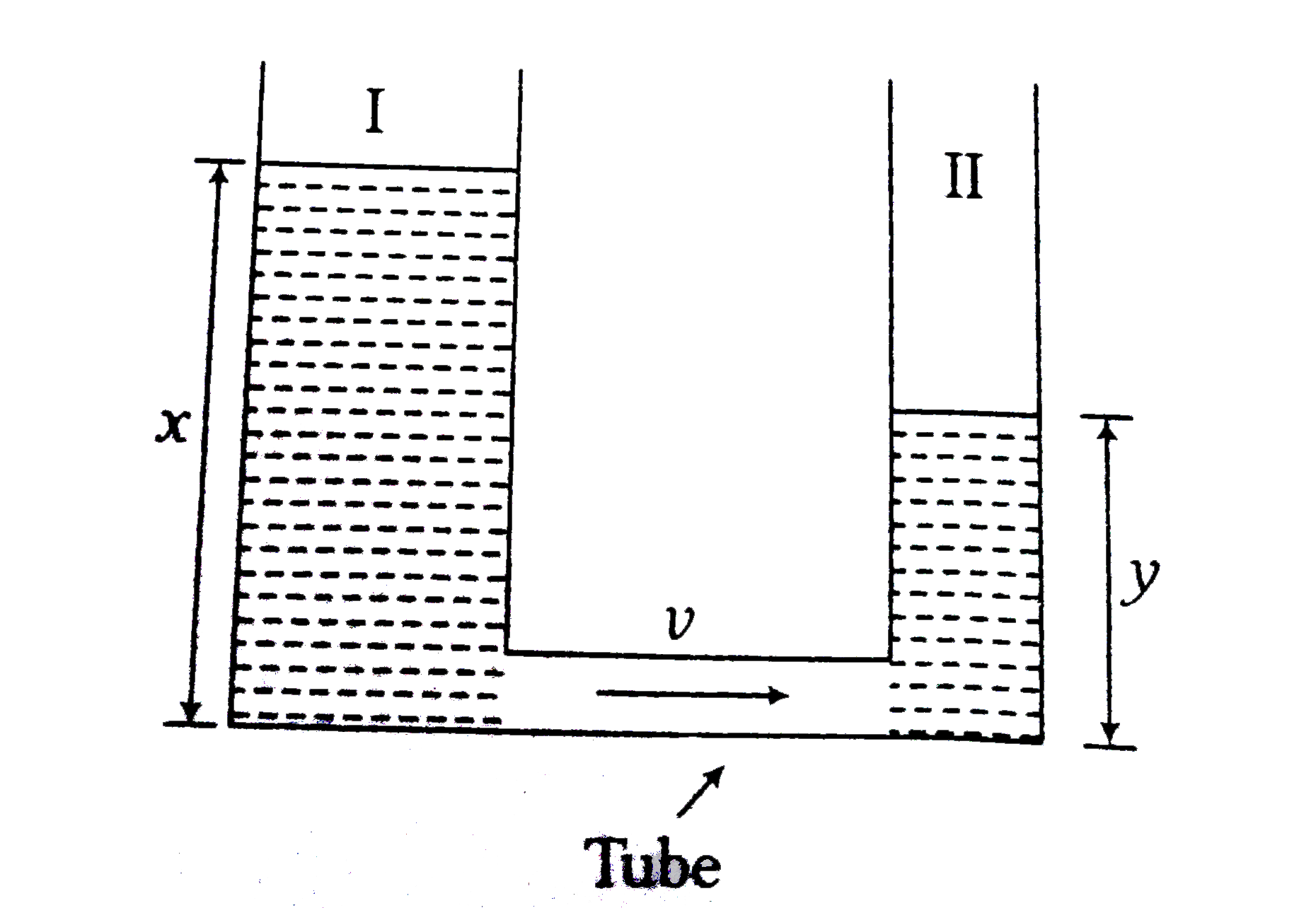
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
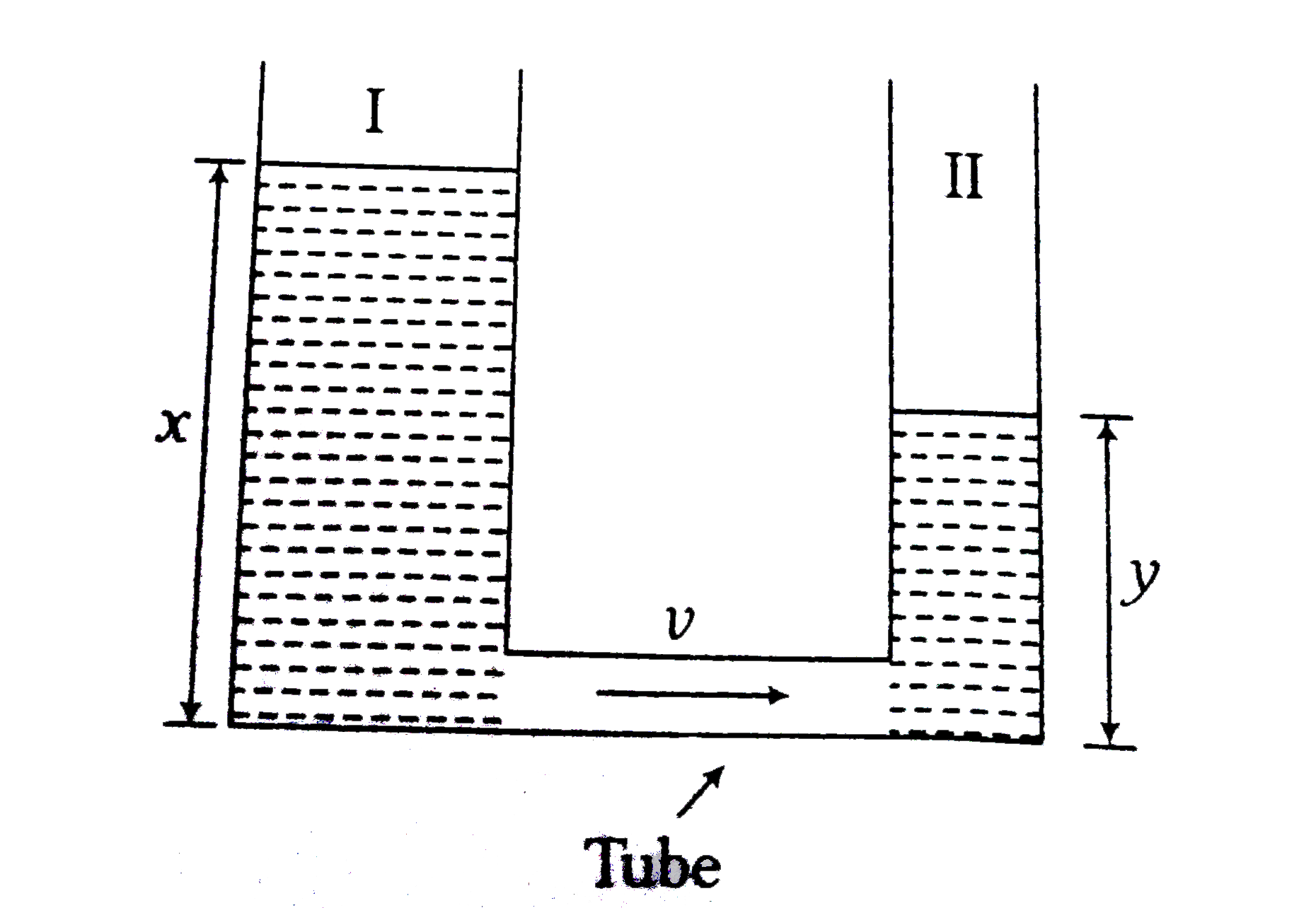
View SolutionAn engine pump is used to pump a liquid of density ρ continuously through a pipe of cross-sectional area A. If the speed of flow of the liquid in the pipe is v, then the rate at which kinetic energy is being imparted to the liquid is
View Solution
