If from a variable point P representing the complex number $z_{1}$ on the curve $| z | = 4$ , two tangents are drawn to the curve $| z | = 2$ , meeting it at points $Q (z_{2})$ and $R (z_{3})$ , then which of the following statement(s) is(are) correct?

A

Triangle , PQR is isosceles.

B

The locus of centroid of triangle PQR is |z|=1.

C

The circumradium of triangle PQR is 2.

D

The radius of circle inscribed in triangle PQR is 1.

Text Solution

Verified by Experts

The correct Answer is:C, D

$∴$ From above figure , $cos (∠ P O R) = \frac{O R}{O P} \frac{2}{4} = \frac{1}{2}$
$\Rightarrow ∠ P O R = \frac{π}{3} = ∠ P O Q \Rightarrow ∠ O P R = ∠ O P Q = 30^{\circ}$
$\Rightarrow ∠ Q P R = 60^{\circ} ... . . (1)$
Also, in $Δ P Q R, P Q = P R ... . . (2)$
$∴$ From (1) and (2) , we get
$Δ P Q R$ is equilateral $\Rightarrow$ (A) is incorrect.
Also, PQOR are concyclic and $∠ O Q P and ∠ O R P = 90^{\circ}$ .
So, circumcentre of $Δ P Q R$ passes through O(0,0) and OP is diameter of it.
So, circumcentre of $Δ P Q R$ = mid point of OP
$= (\frac{0 + 4 cos θ}{2}, \frac{0 + 4 sin θ}{2}) = (2 cos θ, 2 sin θ)$
=centroid of $Δ P Q R$ [As, $Δ P Q R$ is equilateral.]
$∴$ The locus of centroid of $Δ P Q R$ is |z|=2 $\Rightarrow$ (B) is incorrect.
Also, circumradius of $Δ P Q R = \frac{O P}{2} = \frac{4}{2} = 2 \Rightarrow$ (C) is correct.
As, $r = \frac{R}{2} = \frac{2}{2} = 1$ (As, $Δ P Q R$ is equilateral.)
$\Rightarrow$ radius of circle inscribed in $Δ P Q R$ is 1. $\Rightarrow$ (D) is correct.]

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The points representing the complex numbers z for which ${| z + 4 |}^{2} - {| z - 4 |}^{2} = 8$ lie on
Aa straight line parallel to x-axis
Ba straight line parallel to y-axis
Ca circle with center as origin
Da circle with center other than the origin.
Question 2 - Select One
If $z \neq 1$ and $\frac{z^{2}}{z - 1}$ is real, the point represented by the complex numbers z lies
Aeither on the real axis or on a circle passing thorugh the origin.
Bon a circle with centre at the origin.
Ceither on the real axis or an a circle not possing through the origin .
Don the imaginary axis .
Question 3 - Select One
In a given parallelogram, if the points $P_{1}$ and $P_{2}$ represent two complex numbers $z_{1}$ and $z_{2}$ , then the point $P_{3}$ represents the number
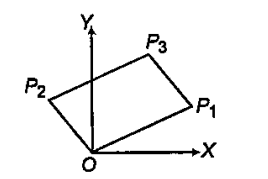A $z_{1} + z_{2}$
B $z_{1} - z_{2}$
C $z_{1} \times z_{2}$
D $z_{1} + z_{2}$

BANSAL-TEST PAPERS-MATHS

Home
Ask Doubt
Profile