Discuss atom as a magnetic dipole. Hence define Bohr magneton.

Text Solution

Verified by Experts

Atom as a Magnetic Dipole
Every atom consists of a central part, called nucleus, where the entire mass and positive charge of the atom are concentrated. An equal number of negative charges (i.e. electrons) revolve around the nucleus in circular orbits.
The revolution of electron i.e., negative charge in anticlockwise direction is equivalent to conventional current I in the clockwise direction. The upper face with clockwise current acts as south pole and the lower face acts as north pole. Thus an electron revolving in an orbit is equivalent to a magnetic dipole.

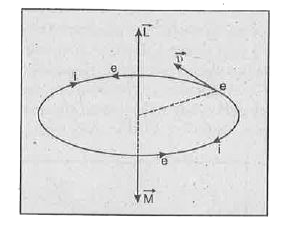
Suppose e is the charge on an electron revolving in a circular orbit of radius r with a uniform angular velocity, $ω$ .
If T is the time period of revolution of the electron, then
Current = $\frac{charge}{time}$
or $I = \frac{e}{T}$
= $\frac{e}{2 π / ω} (∵ T = \frac{2 π}{ω})$
or $I = \frac{e ω}{2 π} ... (1)$
If M is the magnetic dipole moment of the magnetic dipole
M = IA
Using (1), and putting $A = π r^{2}$ , we get
$M = \frac{e ω}{2 π} π r^{2}$
$M = \frac{1}{2} e ω r^{2} ... (2)$
Relation between orbital angular momentum and magnetic dipole momentum.
Because of orbital motion, the revolving electron has an orbital angular momentum L given by
$L = m v r = m r ω r = m ω r^{2}$
$∴$ From (2),
$M = \frac{1}{2} \frac{e}{m} m ω r^{2}$
$M = \frac{1}{2} \frac{e}{m} L$
In vector form,
$\to M = - (\frac{e}{2 m}) \to L ... (3)$
This shows that like $\to L$ , magnetic dipole moment $\to M$ of the atom is perpendicular to the plane of the orbit.
Negative sign shows that direction of $\to M$ is opposite to the direction of $\to L$ , as is clear from the figure.
According to Bohr.s theory, an electron cannot revolve in any orbit it likes. It can revolve only in those orbits for which the total angular momentum is an integral multiple of $h / 2 π$ , where h is the Planck.s constant i.e.
Angular momentum of the electron,
$L = \frac{n h}{2 π}$
or $m r^{2} ω = \frac{n h}{2 π}$
(angular momentum, $L = m v \times r = m r ω \times r = m r^{2} ω$ )
where n = 1, 2, 3, ........
$∴ r^{2} ω = \frac{n h}{2 π m} ... (4)$
From (2) and (4),
$M = \frac{e}{2} \cdot \frac{n h}{2 π m} = n \cdot \frac{e h}{4 π m} = n μ_{B} ... (5)$
It is obvious that $\frac{e h}{4 π m}$ is the least value of the magnetic moment. $(μ_{B} = 9.27 \times 10^{- 24} J T^{- 1} or A m^{2})$ .
Bohr Magneton
It is defined as the magnetic dipole moment associated with an electron due to its orbital motion in the first orbit of hydrogen atom.

Updated on:21/07/2023

The correct value of Bohr magneton is
A $9.27 \times 10^{- 24} A m^{2}$
B $9.27 \times 10^{24} A m^{2}$
C $9.27 \times 10^{- 24} A m^{- 2}$
D $9.27 \times 10^{24} A m^{- 2}$
What is the correct value of Bohr magneton?
A $8.89 \times 10^{- 24} A m^{2}$
B $9.27 \times 10^{- 24} A m^{2}$
C $5.56 \times 10^{- 24} A m^{2}$
D $9.27 \times 10^{- 28} A m^{2}$
What is the correct value of Bohr magneton?
A $8.89 \times 10^{- 24} A m^{2}$
B $9.27 \times 10^{- 24} A m^{2}$
C $5.56 \times 10^{- 24} A m^{2}$
D $9.27 \times 10^{- 28} A m^{2}$