Question

State and prove theorem of parallel axes.

Explanation

Theorem of parallel axis : The moment of inertai of a body about an axis is equal to the sum of (i) its moment of inertia about a parallel axis through its centre of mass and (ii) the product of the mass of the body and the square of the distance between the two axes.

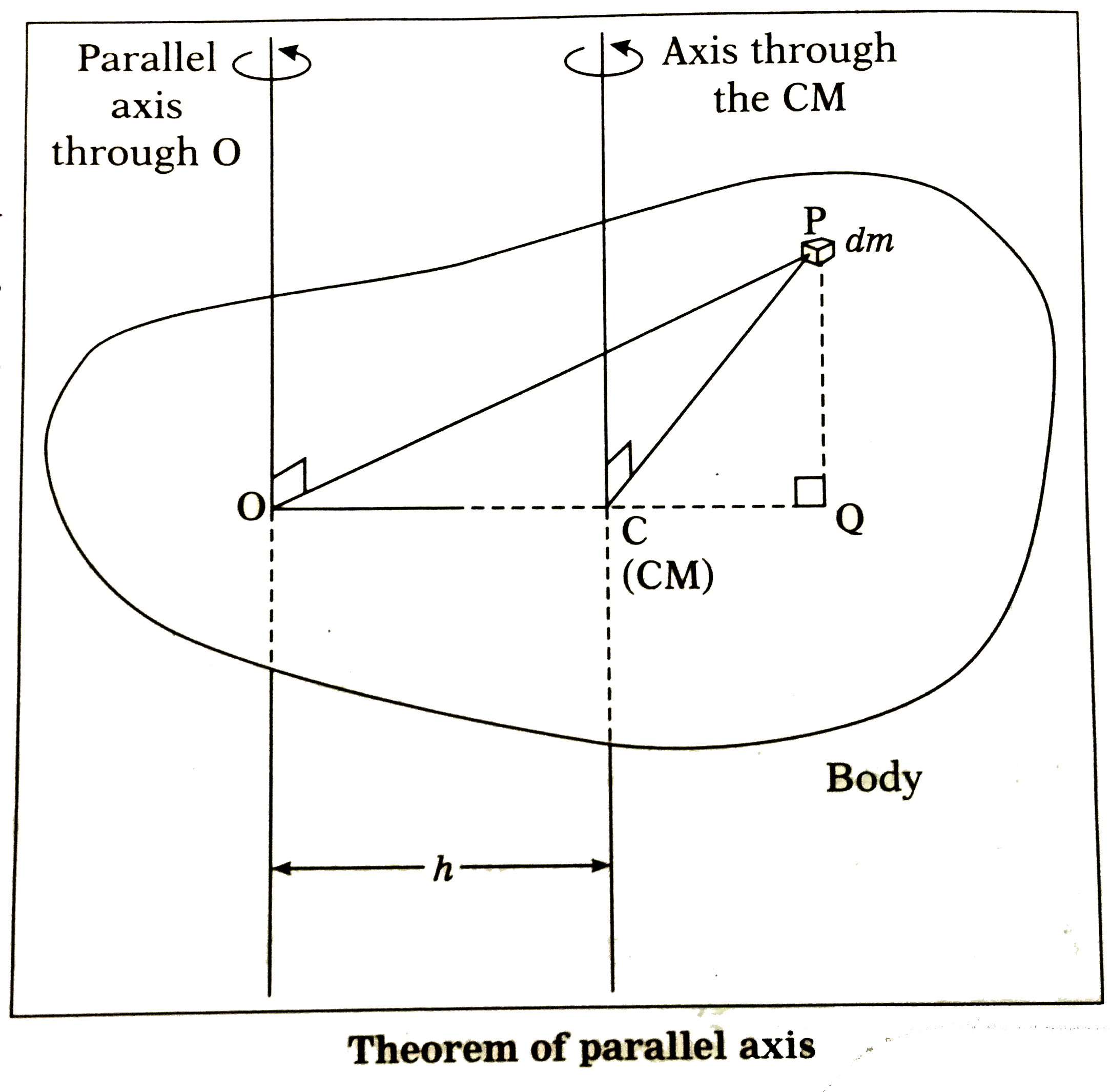
Proof : `I_(CM)` be the moment of inertia (MI) of a body of mass M about an axis thorugh its centre of mass C, and I be its MI about a parallel axis through any point O. If the distance between the two axes is h, them the theorem of parallel axis can be stated mathematically as
`I=I_(CM)+Mh^(2)`
Consider an infinitesimal volume element of mass dm of the body at a point P. It is at a perpendicular distance CP from the rotation axis through C and a perpendicular distance OP from the parallel axis through O.
The MI of the element about the axis through C is `CP^(2)`dm. Therefore, the MI of the body about the axis through the CM is `I_(CM)=int CP^(2)` dm. Similarly ,the MI of the body about the parallel axis through O is `I=int OP^(2)` dm.
Draw PQ perpendicular to OC produced as shown in the figure. Then, from the figure,
`I=int OP^(2)` dm
`=int (OQ^(2)+PQ^(2))dm`
`=int [(OC+CQ)^(2)+PQ^(2)]dm`
`=int (OC^(2)+2OC.OQ+CQ^(2)+PQ^(2))dm`
`=int (OC^(2)+2OC.CP^(2))dm " "(`:'` CQ^(2)+PQ^(2)=CP^(2))`
`=int OC^(2) dm +int 2OC.CQ dm +int CP^(2) dm`
`=OC^(2) int dm +2OC int CQ dm +int CP^(2) dm`
Since, OC=h is constant and `int dm=M` is the mass of the body,
`I=Mh^(2)+2h int dm +I_(CM)`
Now, from the definition of centre of mass, the integral `int CQ` dm gives mass M times a coordinate of the CM with respect to the origin C. Since C is itself the CM, this coorinate is zero and so also the integral.
`:. I=I_(CM)+Mh^(2)`
This proves the theorem of parallal axis.