The internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
Step by step video & image solution for The internal common tangents to two circles with centre C_1 and C_2 intersect the line joining C_1 and C_2 at P and the two direct common tangents intersects the line joining C_1 and C_2 at Q. The length C_1P, C_1C_2 are C_1 Q are in by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
View SolutionThe line joining the points (0,3) and (5,-2) becomes tangent to the curve y=cx+1 then c=
View Solution
Knowledge Check
Two circles with centres at C1,C2 and having radii r1,r2 will intersect each in two real distinct points if , and only if :
Al(C1C2)<r1+r2Bl(C1C2)−|r1−r2|C|r1−r2|<l(C1C2)<r1+r2Dnone of theseThe tangent to the curve y=ex drawn at the point (c,ec) intersects the line joining the points (c−1,ec−1) and (c+1,ec+1)
Aon the left of x=cBon the right of x=0Cat no pointDat all pointsThere are two circles C1 and C2 whose radii are r1,r2, respectively. If distance between their centre is 3r1−r2 and length of direct common tangent is twice of the length of transverse common tangent. Then r1:r2 is:
A5:4B6:5C7:6D8:7
Let C1 be the circle of radius 1 with center at the origin. Let C2 be the circle of radius r with center at the point A=(4,1), where 1<r<3. Two distinct common tangents PQandST of C1 and C2 are drawn. The tangent PQ touches C1 at P and C2 at Q. The tangent ST touches C1 at S and C2 at T. Mid points of the line segments PQandST are joined to form a line which meets the x -axis at a point B . If AB=√5 , then the value of r2 is
View SolutionIn the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equals
View SolutionCircles C1 and C2 are externally tangent and they are both internally tangent to the circle C_3. The radii of C1 and C2 are 4 and 10, respectively and the centres of the three circles are collinear. A chord of C3 is also a common internal tangent of C1 and C2. Given that the length of the chord is m√np where m,n and p are positive integers, m and p are relatively prime and n is not divisible by the square of any prime, find the value of (m+n+p).
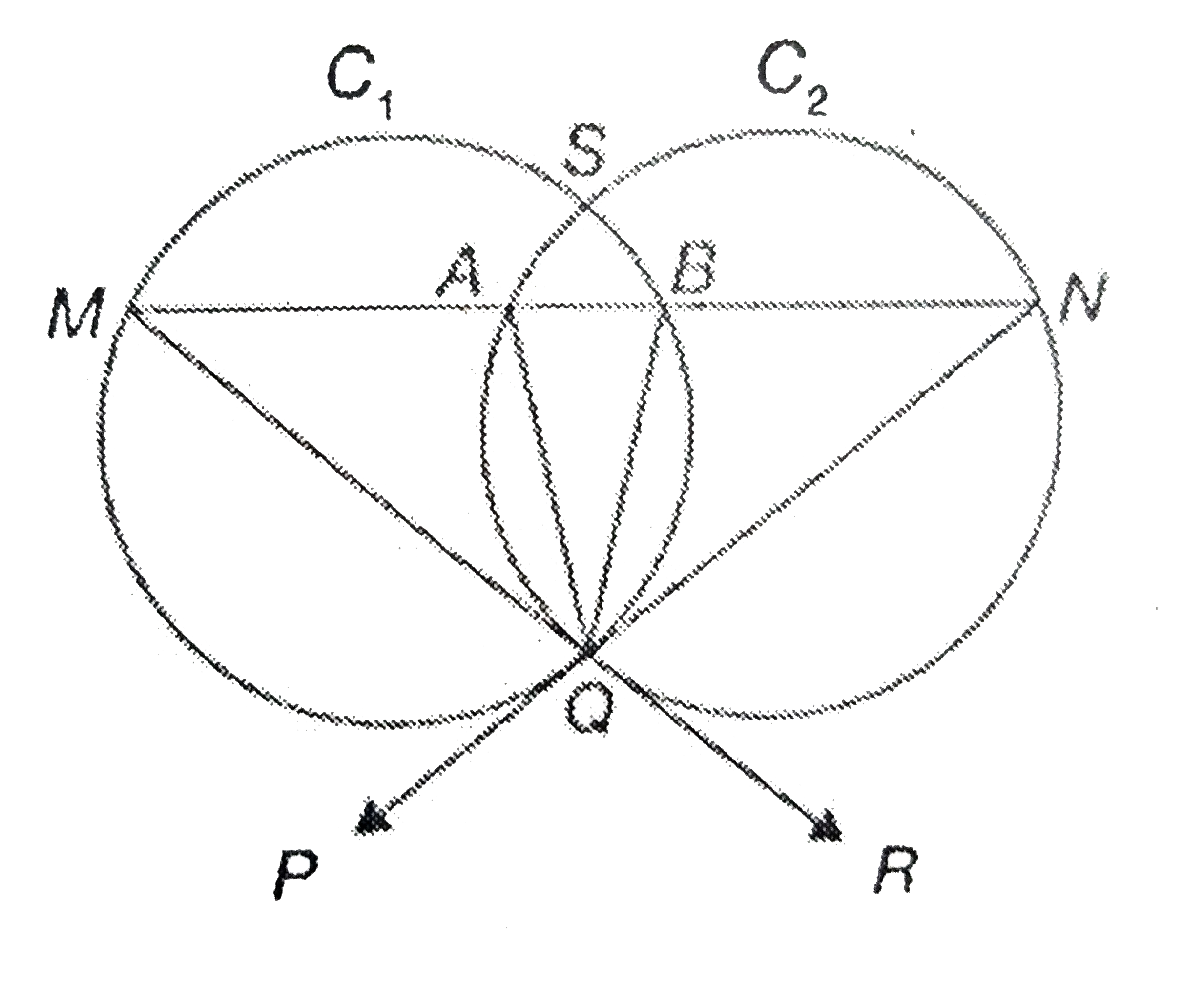
View SolutionIn the given figure (not to scale), two circles C1andC2 intersect at S and Q. PQN and RQM are tangents drawn to C1andC2 respectively at Q. MAB and ABN are the chords of the circles C1andC2. If ∠NQR=85∘, then find ∠AQB.
View SolutionLet R1andR2 be the radil of the circles with centres at C1andC2.
Statement 1: If C1C2≤r1+r2, then the two circles have two common tangents. Because
Statemetn 2: For two common tangents the two circles must intersect in two points.
View Solution
