किसी वैद्युत द्विध्रुव के कारण अक्षीय स्थिति (अनुदैर्घ्य स्थिति) में किसी बिंदु पर वैद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए।
वैद्युत द्विध्रुवय की अक्ष पर स्थित किसी बिंदु पर वैद्युत क्षेत्र की तीव्रता (अक्षीय अथवा अनुदैर्घ्य स्थित)- माना AB वैद्युत द्विध्रुवय K परा वैद्युतांक के माध्यम में स्थित है जिसके A सिरे पर +q आवेश तथा B सिरे पर –q आवेश एक दूसरे से 2l दूरी पर स्थित है। इस वैद्युत द्विध्रुव के मध्य बिंदु O से r मीटर की दूरी पर इसकी अक्षीय में कोई बिंदु P है जहां वैद्युत क्षेत्र की तीव्रता ज्ञात करना है।
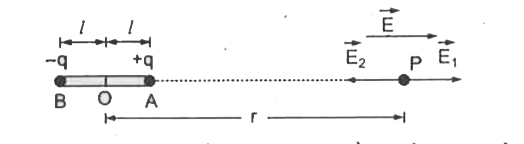
बिंदु P की आवेश +q से दूरी (r-l) और आवेश –q से दूरी (r+l) है। यदि इनके संगत तीव्रताएं क्रमशः E1 व E2 हो तों +q आवेश के कारण बिंदु P पर वैद्युत क्षेत्र की तीव्रता
E1=14πε0Kq(r−l)2 (A→P दिशा में)
-q आवेश के कारण बिंदु P पर वैद्युत क्षेत्र की तीव्रता
E2=14πε0Kq(r+l)2 ( P→B दिशा में)
अतः बिंदु P पर वैद्युत द्विध्रुव के कारण परिणामी वैद्युत क्षेत्र की तीव्रता E=E1−E2
=14πε0Kq(r−l)2–14πε0Kq(r+l)2
=14πε0K[1(r−l)2−1(r+l)2]
=q4πε0K[(r2+l2+2rl)−(r2+l22rl)(r2−l2)2]
=q4πε0K4lr(r2−l2)2=14πε0K2(2ql)r(r2−l2)(2)
परंतु 2ql=p (वैद्युत द्विध्रुव का आघूर्ण) रखने पर E=14πε0K2pr(r2−l2)2
यदि l का मान r की अपेक्षा बहुत कम हो तो l2 का मान r2 की तुलना में नगण्य माना जा सकता है।
E=14πε0K2prr4=14πε0K2pr3 न्यूटन/कूलॉम
यदि वैद्युत द्विध्रुव निर्वात ( अथवा वायु) में रखा है तब K=1 रखने पर बिंदु P पर वैद्युत क्षेत्र की तीव्रता।
E=14πε02pr3 न्यूटन/कूलॉम
इस प्रकार अक्षीय स्थिति में वैद्युत क्षेत्र E की दिशा ऋण आवेश से धन आवेश की ओर को होती है।
Topper's Solved these Questions
- वैद्युत आवेश तथा क्षेत्रBOOK - UP BOARD PREVIOUS YEARCHAPTER - वैद्युत आवेश तथा क्षेत्रEXERCISE - लघु उत्तरीय प्रश्नोत्तर -II
20 Videos
- विधुत-चुम्बकीय तरंगे BOOK - UP BOARD PREVIOUS YEARCHAPTER - विधुत-चुम्बकीय तरंगे EXERCISE - आंकिक प्रश्न
19 Videos
- वैद्युत चुम्बकीय प्रेरणBOOK - UP BOARD PREVIOUS YEARCHAPTER - वैद्युत चुम्बकीय प्रेरणEXERCISE - विस्तृत उत्तरीय प्रश्नोत्तर
12 Videos
Similar Questions
कूलॉम का वैद्युत बल संबंधी नियम लिखिए।
अथवा कूलॉम का विद्युत बल का नियम क्या है?
अथवा दो बिंदु आवशों के बीच लगने वाले आकर्षण अथवा प्रतिकर्षण बल क लिए कूलॉम का सूत्र लिखिए।
View Solutionउन विद्युत-चुम्बकीय तरंगो की तरंगदैर्घ्य ज्ञात कीजिए जिनकी आवृत्ति 6.0×1012 हर्ट्ज़ है। तरंग के प्रकार की पहचान कीजिए।
View Solutionविस्थापन धरा क्या है ? इसकी आवश्यकता क्यों की गयी ? व्याख्या कीजिए | एम्पेयर-मैक्सवेल समीकरण प्राप्त कीजिए |
अथवा विस्थापन धरा क्या है ? इसकी आवश्यकता क्यों महसूस की गयी ?
इसका मात्रक लिखिए |
अथवा विस्थापन धरा से क्या तात्पर्य है ? व्याख्या कीजिए |
अथवा एम्पेयर के प्रिपथीय नियम का मैक्सवेल द्वारा व्याप्कीकरण लिखिए| यह दिखाइए की संधारित्र को आवेशित करने की प्रकिर्या में संधारित्र की प्लेटो के बिच उत्पन्न धरा होती है ?
i=ε0dϕEdt
जहाँ ϕE संधारित्र की प्लेटो को आवेशित करने पर उत्पन्न वैद्युत फ्लक्स है |
अथवा एम्पेयर का परिपथीय नियम क्या है ? एम्पेयर-मैक्सवेल का संशोधित नियम बताइए तथा इसकी सहायता से विस्थापन धरा समझाइए |
View Solutionवैद्युत द्विध्रुव तथा द्विध्रुव का आघूर्ण || वैद्युत द्विध्रुव के कारण क्षेत्र अक्षीय स्थिति में || कुछ प्रश्न
View Solutionवैद्युत द्विध्रुव के कारण क्षेत्र अक्षीय स्थिति में || विद्युत् द्विध्रुव के कारण निरक्षीय स्थिति में क्षेत्र || कुछ प्रश्न | VIPIN SINGH | PHYSICS
View Solutionवैद्युत क्षेत्र में वैद्युत द्विध्रुव | बाह्य क्षेत्र में द्विध्रुव की स्थितिज ऊर्जा
View Solutionआवेशों के निकाय के कारण विद्युत क्षेत्र || वैद्युत द्विध्रुव तथा द्विध्रुव का आघूर्ण || वैद्युत द्विध्रुव के कारण क्षेत्र अक्षीय स्थिति में || कुछ प्रश्न
View Solutionवैद्युत द्विध्रुव के कारण अक्षीय स्थिति में विद्युत् क्षेत्र
View Solutionवैद्युत द्विध्रुव के कारण निरक्षीय स्थिति में विद्युत् क्षेत्र
View Solutionचुम्बकीय द्विध्रुव के कारण अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionचुम्बकीय द्विध्रुव के कारण निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionएक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionबिंदु आवेश के कारण वैद्युत क्षेत्र की तीरवता|वैद्युत बल रेखाएँ|एकसमान तथा असमान वैद्युत क्षेत्र में वैद्युत बल रेखाएं|OMR
View Solutionवैधुत द्विध्रुव|वैधुत द्विध्रुव आघूर्ण|वैधुत द्विध्रुव के कारण अक्षीय स्थिति में वैधुत क्षेत्र|OMR|Summary
View Solutionवैद्युत द्विध्रव प्रश्न|वैद्युत द्विध्रव के कारण निरक्षीय स्थिति में वैद्युत क्षेत्र|OMR|Summary
View Solutionप्रश्न|विद्युत विभव|विभव से सम्बंधित मुख्य बिंदु|विद्युत क्षेत्र में दो बिन्दुओ के मध्य विभवांतर|बिंदु आवेश के कारण विद्युत विभव|वैद्युत द्विध्रुव|वैद्युत द्विध्रुव आघूर्ण|वैद्युत द्विध्रुव के कारण विद्युत क्षेत्र|OMR|Summary
View Solution
