स्थिर वैद्युतिकी में गॉसय के प्रमेय का उल्लेख कीजिए तथा इसे सिद्ध कीजिए।
गॉस का प्रमेय- इस प्रमेय के अनुसार किसी बंद पृष्ठ A से गुजरने वाला वैद्युत फ्लक्स ϕE, उसे पृष्ठ द्वारा परिबद्ध (घिरे हुए) कुल आवेश q का1/ε0 गुना होता है।
अतः वैद्युत फ्लक्स ϕE=q(1ε0)=qε0
परंतु बंद पृष्ठ A से बद्ध कुल वैद्युत फ्लक्स ϕE=∮→E.d→A
अतः ϕE=∫A→E.d→A=aε0
जहां ε0 निर्वात अथवा वायु की वैद्युशीलता है।
उपत्ति- माना कोई बिंदु आवेश +q, किसी बिंदु O पर स्थित है । माना पृष्ठ A पर कोई बिंदु P है जिसकी बिंदु O से दूरी r है। माना पृष्ठ A पर बिंदु P के चारों ओर एक अल्पांश क्षेत्रपुल dA है जिसके संगत क्षेत्रफल वेक्टर d→A है।
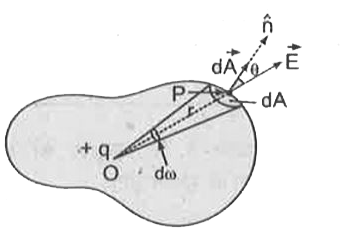
जिसकी दिशा बिंदु P पर अल्पांश क्षेत्रफल dA के बाहर की ओर खींचे गए अभिलम्ब के अनुदिश है।
माना बिंदु O पर रखे बिंदु आवेश +q के कारण बिंदु P पर वैद्युत क्षेत्र की तीव्रता
E=14πε0qr2(O→F)……….1
यदि वैद्युत वेक्टर →E तथा क्षेत्रफल वेक्टर d→A के बीच कोण θ है। तो अल्पांश क्षेत्रफल dA से गुजरने वाला बाहर की ओर दिष्ट वैद्युत फ्लक्स
dθE=→E.dA=EdAcosθ
समीकरण 1 से E का मान रखने पर
dϕE=q4πε0r2dAcosθ
=q4πε0dAcosθr2 ……………2
परंतु dAcosθr2=dω
जहां dω अल्पांश क्षेत्रफल dA द्वारा बिंदु O पर अंतरित घन कोण है। तब समीकरण 2 से dϕE=q4πε0dω
अतः बिंदु आवेश q के कारण संपूर्ण पृष्ठ A से बाहर की और निकलने वाला वैद्युत फ्लक्स
ϕE=∮dϕE=∮q4πε0dω=q4πε0∮dω
परंतु ∮dω, संपूर्ण बंद पृष्ठ क्षेत्रफल A द्वारा बिंदु O पर अंतरित कुल घन कोण है अर्थात ∮dω=4π
अतः ϕE=qε0 यही गॉस की प्रमेय है।
Topper's Solved these Questions
- वैद्युत आवेश तथा क्षेत्रBOOK - UP BOARD PREVIOUS YEARCHAPTER - वैद्युत आवेश तथा क्षेत्रEXERCISE - लघु उत्तरीय प्रश्नोत्तर -II
20 Videos
- विधुत-चुम्बकीय तरंगे BOOK - UP BOARD PREVIOUS YEARCHAPTER - विधुत-चुम्बकीय तरंगे EXERCISE - आंकिक प्रश्न
19 Videos
- वैद्युत चुम्बकीय प्रेरणBOOK - UP BOARD PREVIOUS YEARCHAPTER - वैद्युत चुम्बकीय प्रेरणEXERCISE - विस्तृत उत्तरीय प्रश्नोत्तर
12 Videos
Similar Questions
कूलॉम का वैद्युत बल संबंधी नियम लिखिए।
अथवा कूलॉम का विद्युत बल का नियम क्या है?
अथवा दो बिंदु आवशों के बीच लगने वाले आकर्षण अथवा प्रतिकर्षण बल क लिए कूलॉम का सूत्र लिखिए।
View Solutionउन विद्युत-चुम्बकीय तरंगो की तरंगदैर्घ्य ज्ञात कीजिए जिनकी आवृत्ति 6.0×1012 हर्ट्ज़ है। तरंग के प्रकार की पहचान कीजिए।
View Solutionविस्थापन धरा क्या है ? इसकी आवश्यकता क्यों की गयी ? व्याख्या कीजिए | एम्पेयर-मैक्सवेल समीकरण प्राप्त कीजिए |
अथवा विस्थापन धरा क्या है ? इसकी आवश्यकता क्यों महसूस की गयी ?
इसका मात्रक लिखिए |
अथवा विस्थापन धरा से क्या तात्पर्य है ? व्याख्या कीजिए |
अथवा एम्पेयर के प्रिपथीय नियम का मैक्सवेल द्वारा व्याप्कीकरण लिखिए| यह दिखाइए की संधारित्र को आवेशित करने की प्रकिर्या में संधारित्र की प्लेटो के बिच उत्पन्न धरा होती है ?
i=ε0dϕEdt
जहाँ ϕE संधारित्र की प्लेटो को आवेशित करने पर उत्पन्न वैद्युत फ्लक्स है |
अथवा एम्पेयर का परिपथीय नियम क्या है ? एम्पेयर-मैक्सवेल का संशोधित नियम बताइए तथा इसकी सहायता से विस्थापन धरा समझाइए |
View Solutionयुवा क्रांति के शोले' एकांकी में चित्रित पर्यावरण तथा दहेज प्रशा की समस्याओं का वर्णन कीजिए |
View Solutionसिद्ध कीजिए की (1−4x)1/2 के प्रसार में xr का गुणांक
⌊2r⌊r⌊r है|
View Solutionफलन के लिए रोल प्रमेय का सत्यापन कीजिए
f(x)=e−xsinx,x∈[0,π]
View Solutionफलन f(x)=x2−4xx+2 के लिए अंतराल [0,4] में रोले प्रमेय का सत्यापन कीजिए तथा वह बिंदु ज्ञात कीजिए जहाँ अवकलन शून्य है।
View Solutionf(x)=3+(x−2)23∀x∈[1,3] में रोले प्रमेय के प्रतिबंधो का परीक्षण कीजिए।
View Solutionf(x)=√9−x2,∀x∈[−3,3] के लिए रोले प्रमेय का सत्यापन कीजिए।
View Solutionएक कहानी यह भी' पाठ के आधार पर लिखिका के पिताजी के सकारात्मक और नकारात्मक गुणों का उल्लेख कीजिए।
View Solutionपरीक्षा के दिनों में विद्युत आपूर्ति नियमित न होने से हो रही कठिनाइयों का उल्लेख करते हुए विद्युत प्रदाय संस्थान के मुख्य प्रबंधक को तुरंत इसे ठीक करने का अनुरोध कीजिए।
View Solutionहैलोजन के संबंध में गलत कथन का चयन कीजिए।
View Solutionनिम्नलिखित के बारे में गलत कथन का चयन कीजिए-
View Solutionसूची | का सूची || के साथ मिलान कीजिए तथा सूची के नीचे दिए गए कोड का उपयोग करके सही उत्तर का चयन कीजिए।
View Solutionग्लाइकोलिसिस के बारे में गलत कथन का चयन कीजिए।
View SolutionCO के विषय में गलत कथन का चयन कीजिए।
View Solution
