गाउस के नियम का उपयोग करते हुए एक असीमित विस्तार वाली समतल चादर के निकट विद्युत क्षेत्र की तीव्रता ज्ञात कीजिये।
गॉस का नियमः
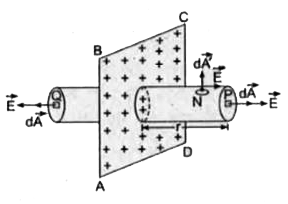
अनन्त विस्तार की समतल आवेशित अचालक प्लेट का कारण वैद्युत क्षेत्र की तीव्रता- माना अनन्त विस्तार की समतल अचालक प्लेट ABCD के एक तल पर धन आवेश समान रूप से वितरित है। माना इस तल के एकांक क्षेत्रफल पर उपस्थित आवेश की मात्रा σ है।
माना आवेशित तल से r दूरी पर कोई बिंदु P है जहां वैद्युत क्षेत्र की तीव्रता त करनी है। माना चादर से दूसरी ओर, चादर से समान दूरी r पर एक अन्य बिंदु Q इस प्रकार है कि रेखा PQ चादर के लम्बवत है।
बिंदु P पर वैद्युत क्षेत्र की तीव्रता ज्ञात करने के लिए हम एक ऐसे बेलनाकार पृष्ठ की कल्पना करते हैं जिसकी अक्ष आवेशित चादर के लम्बवत है। तथा इसके समतल पृष्ठ बिंदु P तथा Q से होकर गुजरते है। माना बेलन के प्रत्येक समतल पृष्ठ का क्षेत्रफल A है। चूंकि बिंदु P तथा Q चादर से समान दूरी पर है अतः दोनों बिंदुओं पर वैद्युत क्षेत्र की तीव्रता परिमाण में समान होगी।
बेलन के समतल पृष्ठ हेतु वैद्युत फ्लक्स
dϕP=dϕQ=→E.d→A=EdAcos0∘=EdA
तथा बेलन के वक्र पृष्ठ हेतु वैद्युत फ्लक्स
dϕN=→E.d→A=EdA’=cos90∘=0
अतः बेलनाकार गॉसीय पृष्ठ से गुजरने वाला कुल वैद्यु फ्लक्स
ϕE=ϕP+ϕQ+ϕN
ϕE=2∫→E.d→A+∫→E.d→A
=2∫EdA+0
=2E∫dA=2EA
परंतु गॉस प्रमेय से
ϕE=1ε0 (गॉसीय पृष्ठ के भीतर स्थित कुल आवेश)
=1ε0 (चादर के क्षेत्रफल A पर आवेश)
=1ε0=2EA अथवा E=σ2ε0
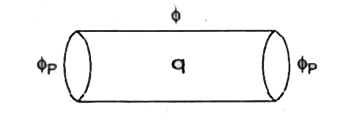
बेलन से बद्ध कुल वैद्युत फ्लक्स =qε0
यदि बेलन के समतल पृष्ठ से बद्ध वैद्युत फ्लक्स ϕP हो तब बेलन से बद्ध कुल वैद्युत फ्लक्स
ϕP+ϕ+ϕP=qε0
या 2ϕP=qε0−ϕ या ϕP=12(qε0−ϕ)
Topper's Solved these Questions
- वैद्युत आवेश तथा क्षेत्रBOOK - UP BOARD PREVIOUS YEARCHAPTER - वैद्युत आवेश तथा क्षेत्रEXERCISE - लघु उत्तरीय प्रश्नोत्तर -II
20 Videos
- विधुत-चुम्बकीय तरंगे BOOK - UP BOARD PREVIOUS YEARCHAPTER - विधुत-चुम्बकीय तरंगे EXERCISE - आंकिक प्रश्न
19 Videos
- वैद्युत चुम्बकीय प्रेरणBOOK - UP BOARD PREVIOUS YEARCHAPTER - वैद्युत चुम्बकीय प्रेरणEXERCISE - विस्तृत उत्तरीय प्रश्नोत्तर
12 Videos
Similar Questions
कूलॉम का वैद्युत बल संबंधी नियम लिखिए।
अथवा कूलॉम का विद्युत बल का नियम क्या है?
अथवा दो बिंदु आवशों के बीच लगने वाले आकर्षण अथवा प्रतिकर्षण बल क लिए कूलॉम का सूत्र लिखिए।
View Solutionउन विद्युत-चुम्बकीय तरंगो की तरंगदैर्घ्य ज्ञात कीजिए जिनकी आवृत्ति 6.0×1012 हर्ट्ज़ है। तरंग के प्रकार की पहचान कीजिए।
View Solutionविस्थापन धरा क्या है ? इसकी आवश्यकता क्यों की गयी ? व्याख्या कीजिए | एम्पेयर-मैक्सवेल समीकरण प्राप्त कीजिए |
अथवा विस्थापन धरा क्या है ? इसकी आवश्यकता क्यों महसूस की गयी ?
इसका मात्रक लिखिए |
अथवा विस्थापन धरा से क्या तात्पर्य है ? व्याख्या कीजिए |
अथवा एम्पेयर के प्रिपथीय नियम का मैक्सवेल द्वारा व्याप्कीकरण लिखिए| यह दिखाइए की संधारित्र को आवेशित करने की प्रकिर्या में संधारित्र की प्लेटो के बिच उत्पन्न धरा होती है ?
i=ε0dϕEdt
जहाँ ϕE संधारित्र की प्लेटो को आवेशित करने पर उत्पन्न वैद्युत फ्लक्स है |
अथवा एम्पेयर का परिपथीय नियम क्या है ? एम्पेयर-मैक्सवेल का संशोधित नियम बताइए तथा इसकी सहायता से विस्थापन धरा समझाइए |
View Solutionकूलम्ब नियम पर कुछ प्रश्न || विद्युत क्षेत्र एवं विद्युत् क्षेत्र की तीव्रता || वैद्युत क्षेत्र रेखाएँ ||
View Solutionविद्युत क्षेत्र का भौतिक अभिप्राय || बिंदु आवेश के कारण विद्युत् क्षेत्र || आवेशों के निकाय के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionएकसमान आवेशित अनंत समतल चादर के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionआवेशित वलय के कारण विद्युत क्षेत्र की तीव्रता
View Solutionकूलम्ब नियम पर कुछ प्रश्न || विद्युत क्षेत्र एवं विद्युत् क्षेत्र की तीव्रता || वैद्युत क्षेत्र रेखाएँ
View Solutionएकसमान आवेशित अनंत समतल चादर के कारण विद्युत क्षेत्र
View Solutionचुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता | एक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता
View Solutionएक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionअनंत लंबाई के एकसमान आवेशित सीधे के कारण विद्युत क्षेत्र |एकसमान आवेशित अनंत समतल चादर के कारण विद्युत क्षेत्र |प्रश्न |OMR|Summary
View Solutionगोले के कारण विद्युत क्षेत्र ज्ञात करना
View Solutionकूलॉम के नियम पर महत्वपूर्ण उदाहरण |विद्युत क्षेत्र |विद्युत क्षेत्र की दिशा |विद्युत बल एवं विद्युत क्षेत्र मे संबंध | विद्युत क्षेत्र का अध्यारोपण |OMR|Summary
View Solutionचकती और अनंत चादर के कारण विद्युत क्षेत्र
View Solutionगाउस का नियम|गाउस के नियम के अनुप्रयोग|ठोस चालक अथवा खोखले गोले के कारण विद्युत् क्षेत्र|OMR |Summary
View Solution
