गॉस प्रमेय की सहायता से एकसमान रूप से आवेशित अनन्‍ लम्बाई के सीधे तार के निकट वैद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए।
अथवा गॉस के नियम से एक अनन्त लम्बाई के आवेशित तार के कारण किसी बिंदु पर वैद्युत क्षेत्र की तीव्रता के लिए व्‍यंजक प्राप्त कीजिए।
अथवा गॉस नियम की सहायता से एक आवेशित लंबे तार के निकट वेद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए । तार का रेखीय आवेश घनत्व $λ$ कूलॉम/मीटर है।

Video Solution

Text Solution

Verified by Experts

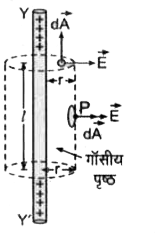
अनन्त लम्बाई के एकसमान आवेशित तार के कारण वैद्युत क्षेत्र की तीव्रता- माना अनन्त लम्बाई का एक तार YY’ है जिस पर धन आवेश एकसमान रूप से वितरित है। माना तार से r दूरी पर कोई बिंदु P है। जहां पर इस तार के कारण वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है।
इसके लिए बिंदु P से गुजरने वाले, त्रिज्या r तथा l लम्बाई का गॉसीय पृष्ठ खींचते हैं। सममिति के कारण इस पृष्ठ के प्रत्येक बिंदु पर वैद्युत क्षेत्र की तीव्रता E समान होगी। यदि वक्र पृष्ठ पर स्थित बिंदु P पर कोई क्षेत्रफल वेक्टर $d \to A$ लिया जाए तो उस बिंदु पर वैद्युत क्षेत्र की तीव्रता $\to E$ तथा क्षेत्रफल वेक्टर $d \to A$ एक ही दिशा में होंगें अर्थात इनके बीच कोण शून्य होगा।
क्षेत्रफल अवयव $d A$ से होकर जाने वाल वैद्युत फ्लक्स
$d ϕ_{E} = \to E . d \to A = E d A {cos 0} = E d A$
गॉसीय पृष्ठ से गुजरने वाला वैद्युत फ्लक्स
$ϕ_{E} = \int_{A} \to E . D \to A = \int_{A} E d A = E \int_{A} d A$
परंतु $\int_{A} d A = 2 π r l$ [बेलन के वक्र पृष्ठ का क्षेत्रफल $= 2 π r l$ ]
अतः $ϕ_{E} = (2 π r)$
गॉस प्रमेय
$ϕ_{E} = \frac{1}{ε_{0}}$ (बेलनाकार पृष्ठ के भीतर स्थित कुल ओवश)
$= \frac{1}{ε_{0}}$ (तार की l लम्बाई पर स्थित आवेश) $= \frac{1}{ε_{0}} λ l$
अतः $E (2 π r l) = \frac{1}{ε_{0}} λ l$
अतः आवेशित तार से r दूरी पर वैद्युत क्षेत्र की तीव्रता
$E = \frac{λ}{2 π ε_{0} r} = \frac{1}{4 π ε_{0}} \frac{2 λ}{r}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

UP BOARD PREVIOUS YEAR-वैद्युत आवेश तथा क्षेत्र-विस्तृत उत्तरीय प्रश्नोत्तर

Home
Ask Doubt
Profile