If ABCD be a rectangle and P, Q, R, S be the mid-points of AB, BC, CD and DA respectively, then the area of the quadrilateral PQRS is equal to
13 are (ABCD)
34 area (ABCD)
12 area (ABCD)
area (ABCD)
The correct Answer is:C
To find the area of the quadrilateral PQRS formed by the midpoints of the sides of rectangle ABCD, we can follow these steps:
Step 1: Define the dimensions of the rectangle
Let the length of rectangle ABCD be 2x and the breadth be 2y.
Step 2: Identify the midpoints
The midpoints of the sides are:
- P is the midpoint of AB
- Q is the midpoint of BC
- R is the midpoint of CD
- S is the midpoint of DA
From the dimensions:
- AP=PB=2x2=x
- BQ=QC=2y2=y
- CR=RD=x
- DS=SA=y
Step 3: Calculate the area of rectangle ABCD
The area of rectangle ABCD is given by:
AreaABCD=Length×Breadth=2x×2y=4xy
Step 4: Calculate the area of triangles formed
The quadrilateral PQRS is formed by the midpoints, and we can see that it divides the rectangle into four triangles:
1. Triangle APS
2. Triangle PBQ
3. Triangle QCR
4. Triangle RDS
The area of each triangle can be calculated as:
Area of each triangle=12×base×height=12×x×y
Since there are four such triangles, the total area of the triangles is:
Total area of triangles=4×(12×x×y)=2xy
Step 5: Calculate the area of quadrilateral PQRS
The area of quadrilateral PQRS is the area of rectangle ABCD minus the area of the four triangles:
AreaPQRS=AreaABCD−Total area of triangles=4xy−2xy=2xy
Conclusion
Thus, the area of quadrilateral PQRS is:
AreaPQRS=2xy
Let the length of rectangle ABCD be 2x and the breadth be 2y.
The midpoints of the sides are:
- P is the midpoint of AB
- Q is the midpoint of BC
- R is the midpoint of CD
- S is the midpoint of DA
- AP=PB=2x2=x
- BQ=QC=2y2=y
- CR=RD=x
- DS=SA=y
The area of rectangle ABCD is given by:
AreaABCD=Length×Breadth=2x×2y=4xy
The quadrilateral PQRS is formed by the midpoints, and we can see that it divides the rectangle into four triangles:
1. Triangle APS
2. Triangle PBQ
3. Triangle QCR
4. Triangle RDS
Area of each triangle=12×base×height=12×x×y
Since there are four such triangles, the total area of the triangles is:
Total area of triangles=4×(12×x×y)=2xy
The area of quadrilateral PQRS is the area of rectangle ABCD minus the area of the four triangles:
AreaPQRS=AreaABCD−Total area of triangles=4xy−2xy=2xy
Thus, the area of quadrilateral PQRS is:
AreaPQRS=2xy
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.145videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2100videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)52videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
Let ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionIn the given figure, if ABCD is a rectangle and P, Q are the mid-points of AD, DC respectively. then, the ratio of lengths PQ and AC is equal to
View Solution19. ABCD is a rectangle having length (x 1) and breadth (x- 1). If P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively, then the perimeter of quadrilateral PQRS is
View SolutionIn the given figure, ABCD is a rectangle in which AB = 40 cm and BC = 25 cm. If P. Q, R, S be the midpoints of AB, BC, CD and DA respectively, find the area of the shaded region.
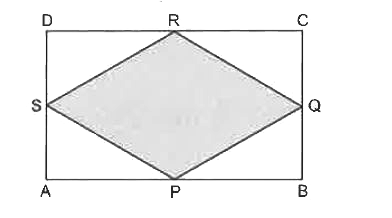 View Solution
View SolutionABCD is a rectangle and E F G and H are the mid-points of AB BC CD DA respectively Prove that EFGH is a rhombus
View SolutionIn the given figure, ABCD is a rectangle in AB−40cmandBC=25cm. If P,Q,R,S be the mid-points of the sides AB,BC,CDandDA respectively, find the area of the shaded region.
View SolutionABCD is a rectangle formed by the points A(1, 1),B(1, 4),C(5, 4) and D(5, 1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? A rectangle? or a rhombus? Justify your answer.
View SolutionABCD is a rhombus and P,Q,R,S are the mid-points of AB,BC,CD,DA respectively. Prove that PQRS is a rectangle.
View Solution

