The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that
AP. CP = BP. DP
AP.BP = CP. DP
AP. CD = AB. CP
BP. AB = CD.CP
The correct Answer is:B
To solve the problem regarding the cyclic quadrilateral ABCD and the intersection of its diagonals AC and BD at point P, we will follow these steps:
1. Understanding Cyclic Quadrilaterals:
A cyclic quadrilateral is a four-sided figure where all vertices lie on the circumference of a circle. This implies that opposite angles of the quadrilateral are supplementary.
2. Identifying the Angles:
When diagonals AC and BD intersect at point P, we can denote the angles formed at P. Let:
- ∠APB = x
- ∠CPD = y
- ∠BAP = z
- ∠DCP = w
3. Using the Property of Angles in Cyclic Quadrilaterals:
In a cyclic quadrilateral, the angles subtended by the same arc are equal. Thus, we have:
- ∠APB = ∠CPD (angles subtended by arc AB)
- ∠BAP = ∠DCP (angles subtended by arc CD)
4. Establishing Angle Relationships:
From the above properties, we can say:
- x = y (since they subtend the same arc)
- z = w (since they subtend the same arc)
5. Conclusion:
Therefore, we can conclude that:
- The triangles APB and DPC are similar by the AA (Angle-Angle) criterion, since they have two pairs of equal angles.
Final Statement:
Thus, it is always true that the angles formed at the intersection of the diagonals of a cyclic quadrilateral maintain the property of equality based on the arcs they subtend.
A cyclic quadrilateral is a four-sided figure where all vertices lie on the circumference of a circle. This implies that opposite angles of the quadrilateral are supplementary.
When diagonals AC and BD intersect at point P, we can denote the angles formed at P. Let:
- ∠APB = x
- ∠CPD = y
- ∠BAP = z
- ∠DCP = w
In a cyclic quadrilateral, the angles subtended by the same arc are equal. Thus, we have:
- ∠APB = ∠CPD (angles subtended by arc AB)
- ∠BAP = ∠DCP (angles subtended by arc CD)
From the above properties, we can say:
- x = y (since they subtend the same arc)
- z = w (since they subtend the same arc)
Therefore, we can conclude that:
- The triangles APB and DPC are similar by the AA (Angle-Angle) criterion, since they have two pairs of equal angles.
Thus, it is always true that the angles formed at the intersection of the diagonals of a cyclic quadrilateral maintain the property of equality based on the arcs they subtend.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.145videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2100videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)52videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
The diagonals AC and BD of a cyclic quadrilateral ABCD interest at right angles at E (figure). A line l drawn through E and perpendicular to AB meets CD at F. Prove that F is the mid-point of CD.
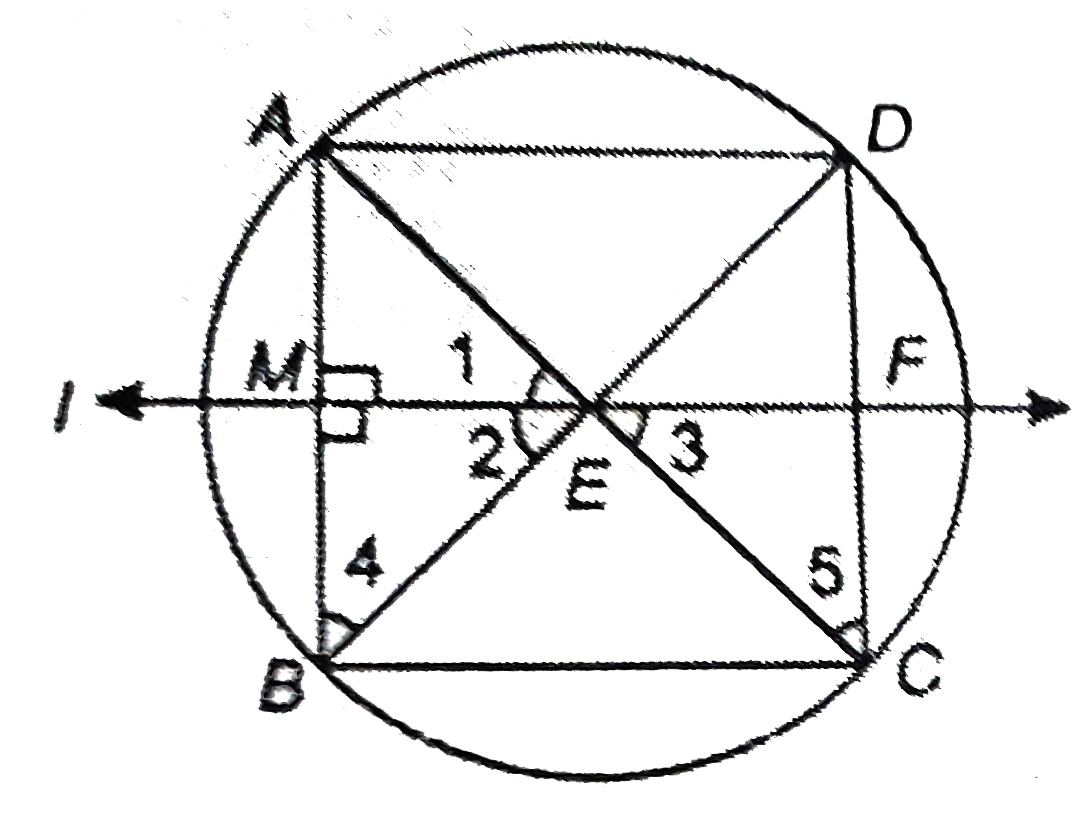 View Solution
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View Solution
Knowledge Check
- Question 1 - Select One
The diagonals AC and BD of a cyclic quadrilateral ABCD inter sect each other at the point P. Then, it is always true that
A(a) BP.AB=CD.CPB(b) AP.CP=BP.DPC(c) AP.BP=CP.DPD(d) AP.CD=AB.CP - Question 2 - Select One
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
A24∘B86∘C38∘D32∘ - Question 3 - Select One
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
A24∘B86∘C38∘D32∘
Bisectors of two adjacent angles A and B of a quadrilateral ABCD intersect each other at a point P. Which one of the following is correct?
View SolutionThe diagonal of a quadrilateral ABCD intersect each other at the point D such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionThe diagonals AC and BD of a quadrilateral ABCD intersect at point 'O'. If BO = OD, then prove that the areas of ΔABCandΔADC are equal
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, find ∠DBC.
View SolutionThe diagonal BD of a quadrilateral ABCD bisects ∠Band∠D, then :
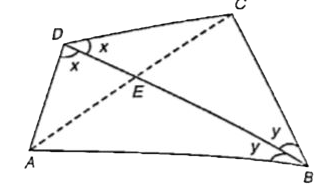 View Solution
View Solution

