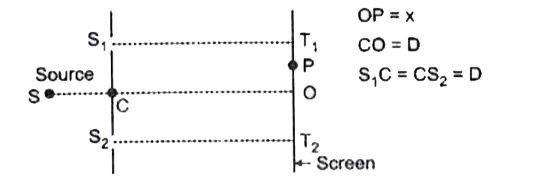
Consider a two slit interferennce arrangements such that the distance of the screen from the slits is half the distance between the slits.That the first minima on the screen falls at a distance D from the centre O, then D is
λ3
λ2
λ2√5
λ√3
The correct Answer is:C
T2P=D+x,T1P=D−x
S1P=√(s1T1)2+(PT1)2
=[D2+(D−x)2]12
S2P=[D2+(D+x)2]12
Minima will occur when
[D2+(D+x)2]12−[D2+(D−x)2]12=λ2
If x = D
[D2+4D2]12=λ2
(5D2)12=λ2,∴D=λ2√5
Topper's Solved these Questions
- WAVE OPTICS BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - MCQ LEVEL - III
10 Videos
- WAVE OPTICS BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - Recent Competitive Questions
18 Videos
- WAVE OPTICS BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - MCQ LEVEL- II (ASSERTIONS)
2 Videos
- WAVE MOTIONBOOK - MODERN PUBLICATIONCHAPTER - WAVE MOTIONEXERCISE - RECENT COMPETITIVE QUESTIONS
18 Videos
- WORK , POWER , ENERGY AND COLLISIONSBOOK - MODERN PUBLICATIONCHAPTER - WORK , POWER , ENERGY AND COLLISIONSEXERCISE - Revision Test
40 Videos
Similar Questions
Consider a two slit interference arrangements such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.

View SolutionConsider a two slit interference arrangements (figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
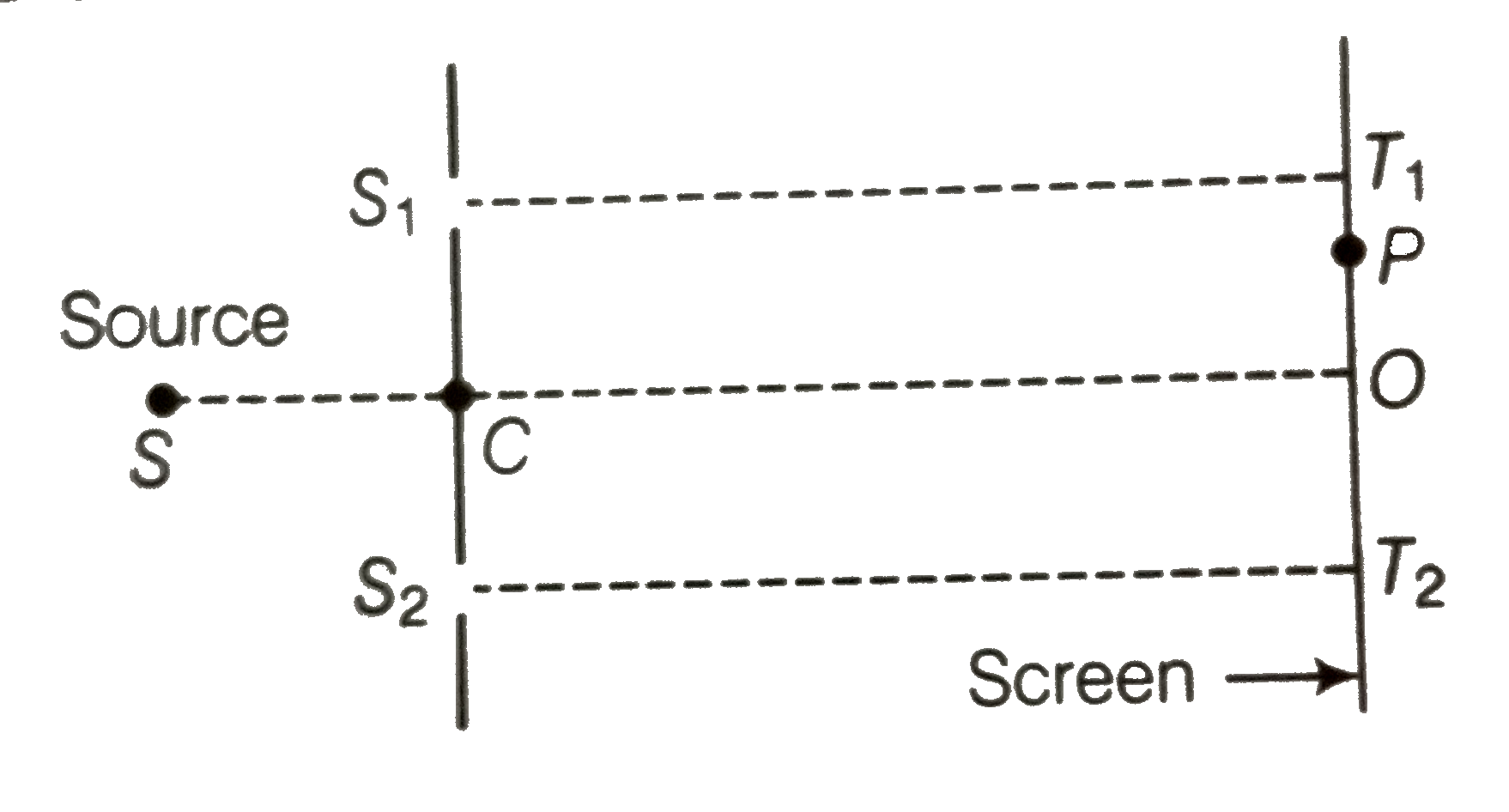
View Solution
Knowledge Check
Consider a two slit interference arrangements (figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
 Aλ2.472Bλ2.236Cλ1.227Dλ3.412
Aλ2.472Bλ2.236Cλ1.227Dλ3.412In a YDSE arrangement, the distance of screen from the slits is half the distance between the slits. If 'λ' is the wavelength of then the value of D such that first minima on the screen falls at a distance D from then centre 'O' is
 AD=λ√5BD=λ2CD=λ5√2DD=λ2√5
AD=λ√5BD=λ2CD=λ5√2DD=λ2√5In Young's experiment, the distance between the slits is 0.025 cm and the distance of the screen from the slits is 100 cm. If two distance between their second maxima in cm is
A0.048B0.096C0.12D0.192
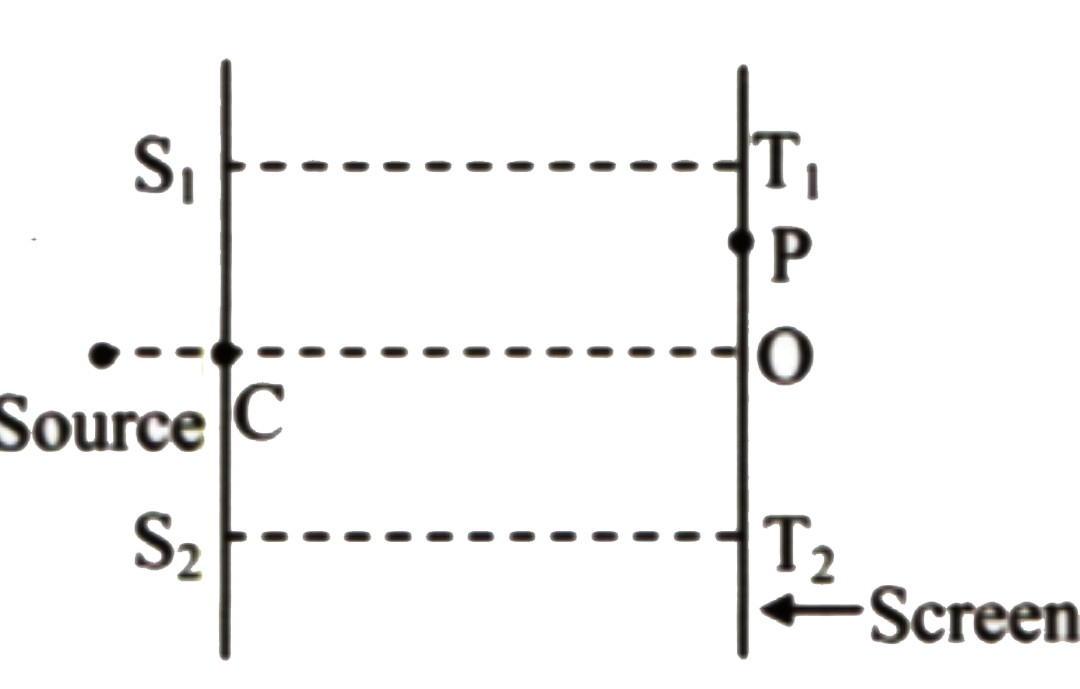
Consider a two slit interference arrangements (figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.

View SolutionIn a special arrangement of Young's double - slits d is twice the distance between the screen and the slits D, i.e. d = 2D. For the setup, the value of D such that the first minima on the screen fall at a distance D from the centre O is found to be λN, where λ is the wavelength of light used. What is the value of N ? [Take √5=2.24]
View SolutionIn a special arrangement of Young's double - slits d is twice the distance between the screen and the slits D, i.e. d = 2D. For the setup, the value of D such that the first minima on the screen fall at a distance D from the centre O is found to be λN, where λ is the wavelength of light used. What is the value of N ? [Take √5=2.24]

View SolutionIn a special arrangement of Young's double - slits d is twice the distance between the screen and the slits D, i.e. d = 2D. For the setup, the value of D such that the first minima on the screen fall at a distance D from the centre O is found to be λN, where λ is the wavelength of light used. What is the value of N ? [Take √5=2.24]

View SolutionIn Young's experiment the distance between the slits is reduced to half and the distance between the slit and screen is doubled then the fringe width
View Solution
