AC = CO = D , S1C=S2C=d<<D
A small transparent slab containing material of μ=1.5 is placed along AS2. What will be the distance from O of the principal maxima

D4
−D5
D10
−D16
The correct Answer is:D
Path difference = 2dsinθ+(μ−1)l
∴ For principal maxima
2dsinθ+0.5l=0
sinθ0=−l4d=−116(∵l=d4)
∴ OP = D tanθ0=−D16
Topper's Solved these Questions
- WAVE OPTICS BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - MCQ LEVEL - III
10 Videos
- WAVE OPTICS BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - Recent Competitive Questions
18 Videos
- WAVE OPTICS BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - MCQ LEVEL- II (ASSERTIONS)
2 Videos
- WAVE MOTIONBOOK - MODERN PUBLICATIONCHAPTER - WAVE MOTIONEXERCISE - RECENT COMPETITIVE QUESTIONS
18 Videos
- WORK , POWER , ENERGY AND COLLISIONSBOOK - MODERN PUBLICATIONCHAPTER - WORK , POWER , ENERGY AND COLLISIONSEXERCISE - Revision Test
40 Videos
Similar Questions
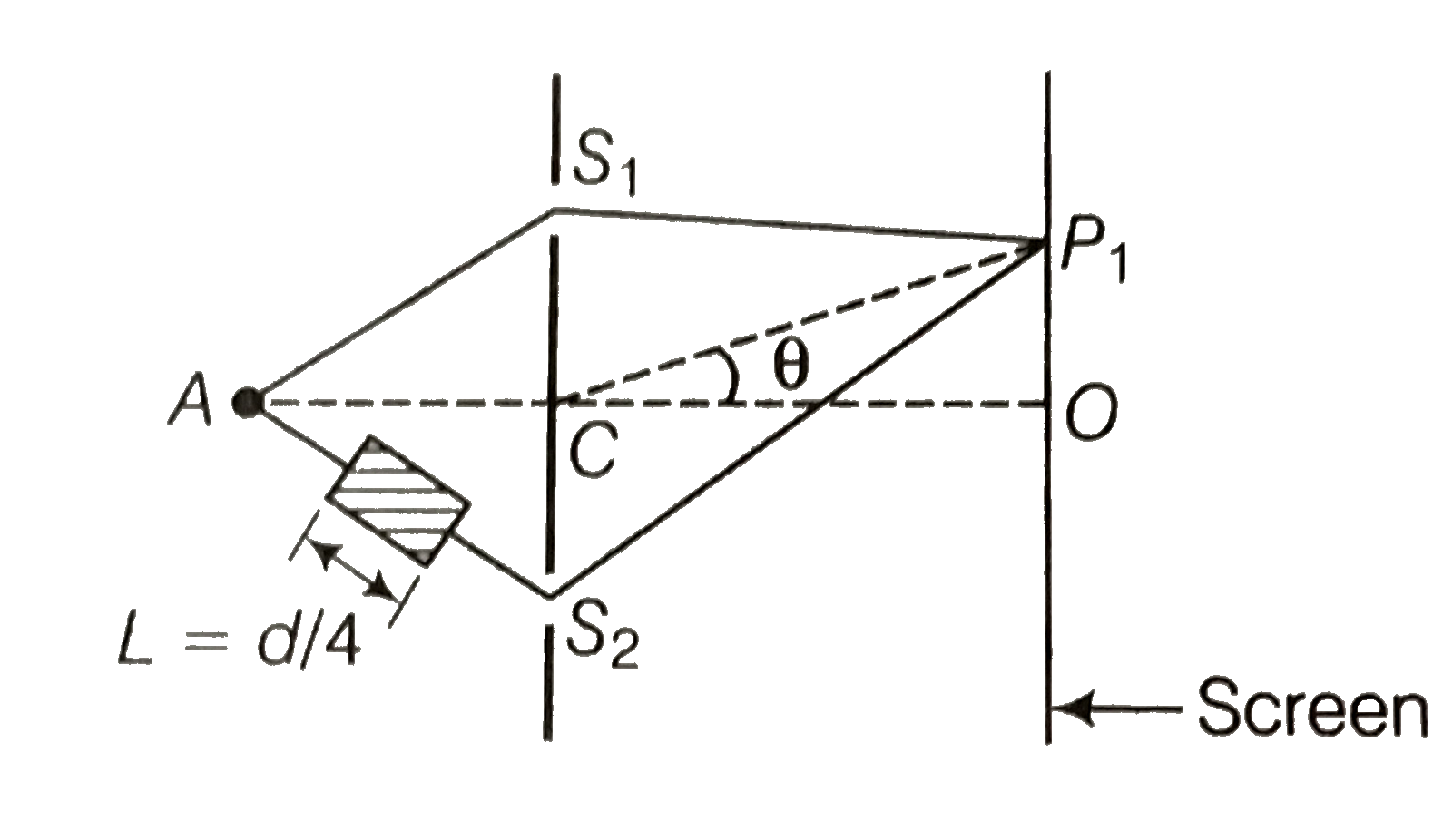
A small transparent slab containing material of μ=1.5 is placed along AS2(figure). What will be the distance from O of the principle maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab ?
View Solution
A small transparent slab containing material of μ=1.5 is placed along AS2(figure). What will be the distance from O of the principle maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab ?
View Solution
Knowledge Check

A small transparent slab containing material of μ=1.5 is placed along AS2(figure). What will be the distance from O of the principle maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab ?A0.19 D and -0.33 DB0.19 D and -0.55 DC0.33 D and -0.65 DD0.33 D and -0.75 DA small transparent slab (μ=1.5) is placed along AS2 as shown.

AC=CO=D,S1C=S2S=d<<D
The distance of princpal maxima front 'O' isAD4BD16CD8DDA small transparent slab (μ=1.5) is placed along AS2 as shown.

AC=CO=D,S1C=S2S=d<<D
The distance of first minima above O isA3D√43BD√247C3D√247D5D√247
In a young’s double slit experiment the distance between slits S1 and S2 is d and distance of slit plane from the screen is D(>>d). The point source of light (S) is placed a distance d2 below the principal axis in the focal plane of the convex lens (L). The slits S1 and S2 are located symmetrically with respect to the principal axis of the lens. Focal length of the lens is f(>>d).
Find the distance of the central maxima of the fringe pattern from the centre (O) of the screen.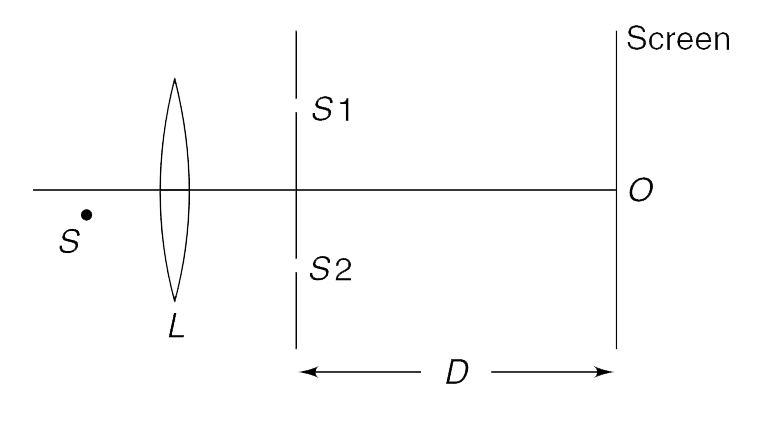
View SolutionTwo transparent sheets of thickness t1 and t2 and refractive indexes μ1 and μ2 are placed infront of the slits in YDSE setup as shown in figure-6.47. If D is the distance of the screen from the slits, then find the distance of zero order maxima from the centre of the screen. What is the condition that zero order maxima is formed at the centre O?

[D[(μ1−1)t1−(μ2−1)t2]d,(μ2−1)t2]
View SolutionLight of wavelengthλ=500nm falls on two narrow slits placed a distance d = 50×10−4 cm
apart, at an angle ϕ=30∘ relative to the slits as shown in figure. On the lower slit a transparent slab of thickness 0.1 mm and refractive index 32 is placed. The interference pattern is observed at a distance D=2m from the slits. Then, calculate

(a) position of the central maxima.
(b) the order of maxima at point C of screen .
(c)how many fringes will pass C, if we remove the transparent slab from the lower slit?
View SolutionA small transparent slab (μ=1.5) is placed along AS2 as shown.

AC=CO=D,S1C=S2S=d<<D
The distance of first minima below the point O is
View SolutionIn YDSE arangement shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000∘Δ (in air). S1 and S2 are two slits separate by d=1mm and D=1m . Left of slits S1andS2 medium of refractive index μ1=2 is presernt refractive index μ2=32 is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of slab μ3 varies with distance from its starting face as shown in figure.

If the thickness of the slab is selected 1μm , then the position of the central maxima will be (y - coordinate)
View Solution
