Prove that −μ1u+μ2v=μ2−μ1R when refraction occurs from rarer to denser medium at a concave spherical refracting surface.
Sign Convention.
(1) All the distances are to be measured from the pole of the surface.
(2) The distances measured in the same direction as the incident light are taken as positive.
(3) The distances measured in the direction opposite to the direction of the incident light are taken as negative.
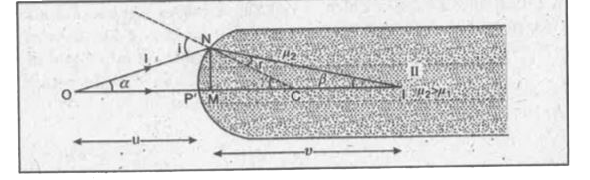
Assumptions. (1) Object is taken as a point object lying on the principal axis.
(2) The aperture of refracting surface is small.
(3) The incident ray from the object strikes the surface at a point very close to point so that angles of incidence and refraction are very small.
Consider a point object O on the principal axis. A ray ON is incident at N and refracts along NI. Another ray OM goes undeviated to meet the previous ray at I. Thus I is the real image of the object O.
Let μ1=Refractive index of medium I
μ2=Refractive index of medium II,
such that
μ2>μ1
For small apertures (namely MN<OM), the problem can easily be solved.
In ΔONC,
i=∠NOM+∠NCM
In ΔONM,
From Snell.s law, for small i and r, we have
sinisinr=ir=μ2μ1
or μ1i=μ2r ...(1)
In ΔNOC,
i=α+β
In ΔNIC,
γ=r+β or r=γ−β
Putting the values of i and r in equation (1), we get
μ1(α+γ)=μ2(γ−β)
or μ1α+μ1γ=μ2γ−μ2β
or μ1α+μ2β=(μ2−μ1)γ ...(2)
Since α,β and γ are small, so they can be replaced by their tangents. So equation (2) becomes
μ1tanα+μ2tanβ=(μ2−μ1)tanγ
or μ1NMMO+μ2NMMI=(μ2−μ1)NMMC
or μ1MO+μ2MI=μ2−μ1MC
Since M is very close to the pole P, So MO≅PO,MI≅PI and MC≅PC
∴μ1PO+μ2PI=μ2−μ1PC
Using sign conventions, PO= - u, PI = v and PC = R, we get
−μ1u+μ2v=μ2−μ1R
or μ2v−μ1u=μ2−μ1R
Topper's Solved these Questions
- BOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - OBJECTIVE TYPE QUESTIONS26videos
OPTICS
- BOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - SHORT ANSWER TYPE QUESTIONS46videos
OPTICS
- BOOK - MBD -HARYANA BOARDCHAPTER - MODEL TEST PAPER - 2EXERCISE - SET - D ( LONG ANSWER TYPE QUESTIONS)4videos
MODEL TEST PAPER - 2
- BOOK - MBD -HARYANA BOARDCHAPTER - PRINCIPLES OF COMMUNICATIONEXERCISE - Objective Type Questions19videos
PRINCIPLES OF COMMUNICATION
Similar Questions
Knowledge Check
- Question 1 - Select One
The relation governing refraction of light from rarer to denser medium at a spherical refracting surface is
A−μ1u+μ2v=μ2−μ1RBμ1u+μ2v=μ2−μ1RCμ1u−μ2v=μ2−μ1RDnone of these - Question 2 - Select One
When a light ray from a rarer medium is refracted into a denser medium, its
ASpeed increases, wavelength increasesBSpeed decreases, wavelength increasesCSpeed increases, wavelength decreasesDSpeed decreases, wavelength decreases - Question 3 - Select One
If μv,μr,μb are refractive indices of violet, red and blue, respectively, in a given medium, then
Aμv=μb=μrBμv>μb<μrCμv>μb>μrDμv>μb<μr
When refraction occurs from denser to……….., then μ2μ1 = …………. .
View SolutionWhen reflection occurs from denser to………….., then μ2μ1=……… .
View SolutionObtain lens maker's formula using the expression n2v−n1u=n2−n1R, propagating from a rarer medium of refractive index (n1) to a denser medium of refractive index (n2) is incident on the convex side of spherical refracting surface of radius of curvature R.
View SolutionFigure shows figure three transparent medi of refractive indices μ1,μ2andμ3. A point object O is placed in the medium μ2. If the entire medium on the right of the spherical surface has refractive index μ1, the image forms at O. If this entire medium has refractive index μ2 the image form at O''. In the situation shown
 View Solution
View SolutionIn the figure shown μ1,μ2,μ3,μ4andμ5 are the refractive indices
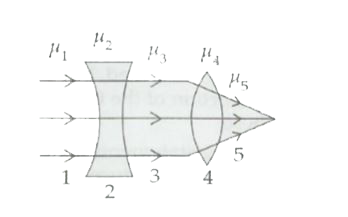
of the mediums 1,2,3,4 and 5 respectively . Consider the following
(1) μ1=μ2 (2) μ3=μ4=μ5
μ2<μ3 (4) μ4>μ5View Solution

