Define fringe width in interference and derive its expression.

Text Solution

Verified by Experts

Fringe Width. It is the distance between any two successive fringes in interference pattern.
Let $S_{1}, S_{2}$ be the two fine slits illuminated by a monochromatic sources of wavelength $λ$ .
Intensity of light at any point P on the screen at a distance D from the slit depends upon the path difference between $S_{2} P$ and $S_{1} P$ .

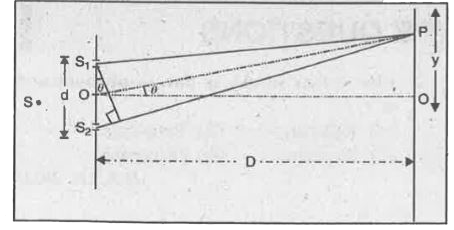
From $S_{1}$ draw $S_{1} A$ perpendicular to $S_{2} P$ . Since $∠ S_{2} S_{1} A \to θ$ [D is very large as compared to d], therefore, $∠ S_{1} A S_{2} \to 90^{\circ}$ and $A P \approx S_{1} P$ .
$∴ Path difference = S_{2} P - S_{1} P = (S_{2} A + A P) - S_{1} P$ or $Path difference = S_{2} A = d sin θ$
Since $θ$ is very small, $sin θ$ can be replaced by $tan θ$ .
$∴ Path difference = d tan θ = d \frac{y}{D}$
Constructive interference [Bright Fringes). For bright fringes, the path difference should be equal to an even multiple of $λ / 2$ .
$∴ \frac{d y}{D} = 2 n \frac{λ}{2} = n λ$
or $y = n \frac{λ D}{d}$
If n = 0, $y_{0} = 0$ , which is the position of central maxima.
If n = 1, $y_{1} = \frac{D}{d} λ$ , which is the position of first maxima.
If n = 2, $y_{2} = \frac{2 D}{d} λ$ , which is the position of
Similarly $y_{n - 1} = (n - 1) \frac{D}{d} λ$
and $y_{n} = n \frac{D}{d} λ$
Fringe width $β = y_{n} - y (n - 1) = \frac{D}{d} λ [n - (n - 1)]$
$β = \frac{D}{d} λ$ ...(i)
Destructive interference [Dark Fringes]. For dark fringes, the path difference should be an old multiple of $1 / 2$ .
$\frac{d}{D} y = (2 n - 1) \frac{λ}{2}$
or $y = \frac{D}{d} (2 n - 1) \frac{λ}{2}$
If n = 1, $y_{1} = \frac{D}{d} \frac{λ}{2}$ , which is the position of 1st minima.
If n = 2, $y_{1} = \frac{D}{d} \frac{2 λ}{2}$ , which is the position of 2nd minima.
If n = 3, $y_{1} = \frac{D}{d} \frac{3 λ}{2}$ , which is the position of 3rd minima.
$∴$ Fringe width, $β = y_{3} - y_{2} = \frac{D}{d} λ$
or $β = \frac{D}{d} λ$ ...(ii)
From (i) and (ii), we conclude that bright and dark fringes have equal fringe width.
$β \propto D$
$\propto λ$
$\propto \frac{1}{d}$
If d = 0, $β = \infty$ i.e. dark and bright bands will be infinitely well spaced and there will be uniform illumination.

Updated on:21/07/2023

|

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

A fringe width of a certain interference pattern is $β = 0.002$ cm What is the distance of 5th dark fringe centre?
A $1 \times 10^{- 2} c m$
B $11 \times 10^{- 2} c m$
C $1.1 \times 10^{- 2} c m$
D $3.28 \times 10^{6} c m$

MBD -HARYANA BOARD-OPTICS-LONG ANSWER TYPE QUESTIONS

Home
Ask Doubt
Profile