Draw a ray diagram to show the formation of the image of an object placed between the optical centre and focus of a convex lens. Deduce the relationship between object distance, image disatnce and focal length of lens.
When object is placed between optical centre and principal focus.
Consider a convex lens of focal length f and optical centre C. Let an object AB be placed perpendicular to the principal axis at a point between C and F. The virtual image of this object A.B. is formed on the same side of the lens. The image is virtual, erect and is behind the object as shown in fig.
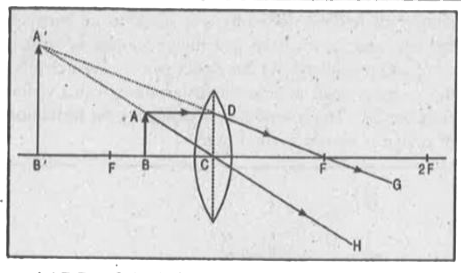
Δ ABC and Δ A.B.C are similar, so
A.B.AB=CB.CB ...(1)
Δ DCF and Δ A.B.F are similar, so
A.B.DC=B.F.CF ...(2)
But DC = AB
∴A.B.AB=B.FCF
From Eqs. (1) & (2), we have
CB.CB=B.FCF
or CB.CB=CB.+CFCF ...(3)
Using sign conventions,
Let CB. = -v, CB = -u, CF = f
So Eq. (3) becomes
−v−u=−v+ff
or vf= - uv + uf
Dividing both sides by uvf, we get
vfuvf=−uvuvf+ufuvf
or 1u=−1f+1v
or 1f=−1u+1v
or −1u+1v=1f
This is lens formula.
Topper's Solved these Questions
- BOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - OBJECTIVE TYPE QUESTIONS26videos
OPTICS
- BOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - SHORT ANSWER TYPE QUESTIONS46videos
OPTICS
- BOOK - MBD -HARYANA BOARDCHAPTER - MODEL TEST PAPER - 2EXERCISE - SET - D ( LONG ANSWER TYPE QUESTIONS)4videos
MODEL TEST PAPER - 2
- BOOK - MBD -HARYANA BOARDCHAPTER - PRINCIPLES OF COMMUNICATIONEXERCISE - Objective Type Questions19videos
PRINCIPLES OF COMMUNICATION
Similar Questions
Draw a ray diagram to show the formation of the image of an object placed between the optical centre and principal focus of a convex lens. Deduce the relationship between the object distance, image distance and focal length under the conditions stated.
View SolutionDraw a ray diagram in each of the following cases to show the formation of image, when the object is placed :
between optical centre and principal focus of a convex lens.View Solution
Knowledge Check
- Question 1 - Select One
The graph shown relationship between object distance and image distance for a equiconvex lens. Then focal length of the lens is
 A0.50±00.5cmB0.50±0.10cmC5.00±0.05cmD5.00±0.10cmu
A0.50±00.5cmB0.50±0.10cmC5.00±0.05cmD5.00±0.10cmu
Draw a ray diagram to show how the image is formed when the object is placed between/and 2/distances from a convex lens. Deduce the relation between the distances of the object and the image from the lens and the focal length of the lens under this condition.
View SolutionWith the help of a ray diagram, show the formation of an image of an object placed between principal focus and centre of curvature of a concave mirror.
View Solution(a) Draw a ray diagram to show the formation of image of an object placed between infinity and optical centre of a concave lens.
(b) A concave lens of focal length 15 cm forms an image 10 cm from the lens. Calculate (i) the object distance, (ii) the nature and magnification of the image formed.View SolutionWrite two characteristics of image formed when an object is placed between the optical centre and focus of a thin convex lens. Draw the graph showing variation of image distance v with object distance u in this case.
View Solution(a) To construct a ray diagram we use two light rays which are so chosen that it is easy to know their directions after reflection. Use these two rays to locate the image of an object placed between infinity and the centre of curvature of a concave mirror.
(b) Draw a ray diagram to show the formation of image of an object placed between the pole and principal focus of a concave mirror. How will the nature and size of the image formed change, if the mirror is replaced by a converging lens of same focal length?View SolutionDraw ray diagrams showing the image formation by a convex lens when an object is placed
(a) between optical centre and focus of the lens
(b) between focus and twice the focal length of the lens
( c) at twice the focal length of the lens
(d) at infinity , (e) at the focus of the lensView SolutionDraw ray diagram showing the image formation by a convex lens when an object is placed at twice the focal length of the lens.
View Solution

