Question

Draw a labelled ray diagram showing the image formation in an astronomical telescope. Define its magnifying power and write expression for it.

Explanation

Telescope. A telescope is an optical instrument used for observing distant objects very clearly.
Astronomical telescope. It produces virtual and inverted image and is used to see heavenly bodies like sun, stars, planets etc. so the inverted image does not affect the observation.
Principle. It is based on the principle that when rays of light are made to incident on an objective from a distant object, the objective forms the real and inverted image at its focal plane. The eye lens is so adjusted that the final image is formed at least distance of distinct vision.
Construction. The refracting type astronomical telescope consists of two convex lenses one of which is called the objective and the other eye piece. The objective is a convex lens of large focal length and large aperture, It is generally a combination of two lenses in contact so as to reduce spherical and chromatic aberrations. The eye piece is also a convex lens but of short focal length and small aperture. The objective is mounted at one end of a brass tube and the eye piece at the other end in a smaller tube which can slide inside the bigger tube carrying the objective.

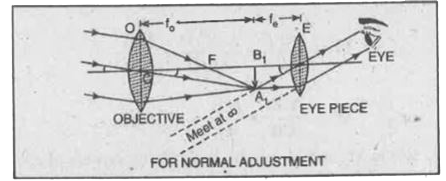
(i) When the final image is formed at infinity. The distance between the image `A_(1)B_(1)` and the eye piece is adjusted equal to the focal length of the eye piece so that the final image is formed at infinity. In this case telescope is said to be in normal adjustment or focussedto infinity. In normal adjustment, distance between two lenses = (`f_(0) + f_(e)`).
 The magnifying power of a telescope in normal adjustment is defined as the ratio of the angle subtended by the image at the eye as seen through the telescope to the angle subtended by the object at the unaided eye, the object and image both lying at infinity.
Angle subtended by object at eye piece or at eye
`/_A_(1)CB_(1) = alpha`
The angle subtended by the image at the eye
`/_B_(1)C_(1)A_(1)=beta`
`:. "Magnifying power", M = (beta)/(alpha)`
As the angles are small, therefore, they can be replaced by their tangents. Hence
`M=(tan beta)/(tan alpha)=(A_(1)B_(1))/(B_(1)C_(1)) xx (B_(1)C)/(A_(1)B_(1))=(B_(1)C)/(B_(1)C_(1))` ...(i)
 When the rays emerging from the eye piece are parallel, the image `A_(2)B_(2)` lies at infinity and the distance `B_(1) C_(1)` is equal to `f_(e)` the focal length of the eye piece, as shown in Fig. Also the distance `B_(1)C=f_(0)` the focal length of the objective.
`:. M=(B_(1)C)/(B_(1)C_(1))=(f_(0))/(f_(e))=("Focal length of the objective")/("Focal length of the eye piece")`
(ii) When final image is formed at least distance of distinct vision.
The objective O forms a real, inverted and diminished image `A_(1)B_(1)` of a far object at focal plane `B_(1)` of the objective in front of the eye piece E. The rays incident on the objective are taken in the form of a parallel beam as they are coming from a far off object. The distance between the eye lens and this image formed is adjusted so that it is less than the focal length of eye piece which, therefore, forms a magnified, virtual image `A_(2)B_(2)` at the least distance of distinct vision.

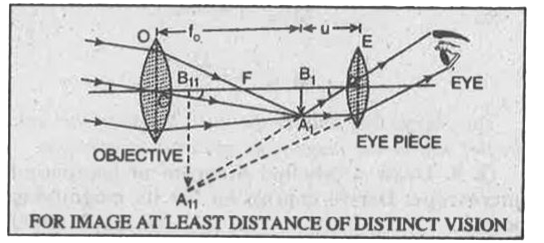
Magnifying power of a telescope is the ratio of angle subtended by the image at the eye formed at least distance of distinct vision to the angle subtended by ihe object (seen directly) at the eye lying at infinity.
Angle subtended at the eye by the image formed at least distance of distinct vision `/_A_(11)C_(1)B_(11) = beta`.
Angle subtended at the eye by the object seen directly lying at infinity
`/_A_(1)CB_(1)=alpha`
`:. "Magnifying power", M =(beta)/(alpha)`
Since `alpha` and `beta` are small, so they can be replaced by their tangents.
`:. M=(tan beta)/(tan alpha)=(A_(1)B_(1) // B_(1)C_(1))/(A_(1)B_(1) // B_(1)C)`
`=(A_(1)B_(1))/(B_(1)C_(1)) xx (B_(1)C)/(A_(1)B_(1))`
`=(B_(1)C)/(B_(1)C_(1))=(f_(0))/(u)` ...(1)
For eye lens,
`-(1)/(u)+(1)/(v)=(1)/(f_(e))`
or `(1)/(u)=(1)/(v)-(1)/(f_(e))=(f_(e)-v)/(vf_(e))`
or `u=(vf_(e))/(f_(e)-v)`
Using sign conventions, we get
`-u=((-D)(f_(e)))/(f_(e)-(-D))=(Df_(e))/(f_(e)+D)`
or `u=(Df_(e))/(f_(e)+D)` ...(2)
Putting eq. (2) in (1), we get
`M=(f_(0)(D+f_(e)))/(Df_(e)=(f_(0))/(f_(e))((D+f_(e))/(D))`
`M= (f_(0))/(f_(e))[1+(f_(e))/(D)]` ...(3)
So, the magnification will be large, if focal length of objective (`f_(0)`) is very large as compared to focal length of eye piece (`f_(e)`).
Since `1 + (f_(e))/(D) gt 1`, so we find that the amplification D produced is more when final image is formed at least distance of distinct vision than when final image is formed at infinity.
In both cases, the final image is inverted hence it is not suitable for seeing terrestrial objects.