मैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
चारो समीकरणों में कौन सी समीकरण यह प्रदर्शित करती है की चुम्बकीय क्षेत्र किसी से उत्सर्जित अथवा समाप्त किया जा सकता है
(a) (i) स्थिरविद्युतिकी के लिए गाउस नियम
(ii) चुम्बकत्व के लिए गाउस नियम
(iii) फ़ैराडे का नियम
(iv) ऐम्पियर-मैक्सवेल का नियम
(b)E का स्रोत q और B का I है। स्पष्टतः, समीकरण (1) और (4) में क्रमश: q और I हैं, जबकि समीकरण (2) और (3) में E और B के स्त्रोत नहीं हैं।
(c) समय से स्वतन्त्र वैद्युत और चुम्बकीय क्षेत्रों के लिए dE/ dt = 0 और dB/ dt = 0 है। इसलिए मैक्सवेल के समीकरण हैं :
(1)∮→E.−→dS=qε0 , (2)∮→B.−→dS=0 , (3) ∮→E.→dl=0 , (4)∮→B.→dl=μ0I
(d) यदि चुम्बकीय एकध्रुव होते, तो समीकरण (2) बदलकर ∮→B.−→dS=μ0q∗m हो जाता अर्थात् यह गाउस नियम जैसा हो जाता। यहाँ qm चुम्बकीय आवेश (अर्थात् चुम्बकीय एकध्रुव तीव्रता) दर्शाता है। समीकरण (3) संशोधित होकर ∮→E.→dl=−ddt∫→B.−→dS+μ0I∗m हो जाता, जहाँ Im , चुम्बकीय आवेशों के प्रवाह के कारण धारा है और वैद्युत आवेशों के प्रवाह के कारण धारा I के अनुरूप है।
(e) समीकरण (2) के अनुसार ∮→B.−→dS=0 अर्थात् किसी बन्द पृष्ठ से सम्बद्ध चुम्बकीय फ्लक्स शून्य होता है। इसका अर्थ है कि चुम्बकीय क्षेत्र रेखाएँ न तो किसी बिन्दु से शुरू होती हैं और न ही किसी बिन्दु पर समाप्त होती हैं बल्कि बन्द लूप बनाती हैं।
(f)समीकरण (3) के अनुसार
∮→E.→dl=−ddl∫→B.−→dS
स्पष्ट है कि ∮→E.→dl≠0 जब तक कि B, समय से स्वतन्त्र न हो। इस प्रकार वैद्युत क्षेत्र रेखाएँ बन्द लूप नहीं बनाती।
Topper's Solved these Questions
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय तरंगे EXERCISE - प्रश्नोत्तरी 1 अंक38videos
वैद्युतचुम्बकीय तरंगे
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय तरंगे EXERCISE - प्रश्नोत्तरी 2 और 3 अंक25videos
वैद्युतचुम्बकीय तरंगे
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय तरंगे EXERCISE - विषय - आधारित समस्याएं : हल सहित10videos
वैद्युतचुम्बकीय तरंगे
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युत विभवEXERCISE - विषय आधारित अभ्यास (प्रतिरूपी अभ्यास)12videos
वैद्युत विभव
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय प्रेरण EXERCISE - NCERT पाठ्यपुस्तक अभ्यास: उत्तरों सहित (अतिरिक्त अभ्यास)3videos
वैद्युतचुम्बकीय प्रेरण
Similar Questions
एक संधारित्र के लिए आवेशन धारा 0.2 A है। विस्थापन धारा क्या है?
02:20View Solutionविस्थापन धारा क्या है? इस विचार को क्यों प्रस्तुत किया गया?
01:52View Solution12 cm व्यासार्ध की एक दूसरे से 5.0mm की दूरी पर रखी दो वृत्ताकार प्लेटों का बना संधारित्र दिखाया गया है। संधारित्र को बाहरी स्रोत से आवेशित किया जा रहा है (जो चित्र में नहीं दिखाया गया)। आवेशन धारा स्थिर और 0.15 A के बराबर है।
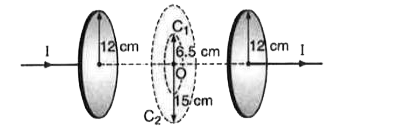
(a) धारिता और प्लेटों के बीच विभवान्तर की परिवर्तन दर निकालें।
(b) प्लेटों के बीच विस्थापन धारा निकालें।
(c) क्या किरखोफ़ का पहला नियम संधारित्र की हर प्लेट पर लागू होता है? व्याख्या करें।02:06View Solutionपृथ्वी पर किसी जगह आसमानी बिजली गिरती है और 1.00×108V के विभवान्तर पर बादल से पृथ्वी को -20.0 C का आवेश देती है।
(a) क्या बादल उच्च विभव पर है या पृथ्वी?
(b) पृथ्वी को कितनी ऊर्जा दी जाती है?
(c) यदि इस ऊर्जा को एक 100 W के बिजली के बल्ब को जलाने के लिए प्रयोग किया जा सकता, तो यह कितने दिन चलेगी?05:40View Solution12cm भुजा वाला एक वर्गाकार लूप, जिसकी भुजाएँ X और Y अक्षों के समान्तर हैं, 8 cm/s के वेग से धनात्मक X-दिशा में ऐसे स्थान में चलाया जाता है जिसमें धनात्मक Z-दिशा में चुम्बकीय क्षेत्र है। क्षेत्र न तो आकाश में एकसमान है और न ही समय के साथ स्थिर। इसकी प्रवणता ऋणात्मक X-दिशा में 10−3T/cm है (अर्थात् ज्यों ज्यों ऋणात्मक X-दिशा में जाएँ, यह 10−3T/cm बढ़ता है) और यह समय के साथ 10−3T/s की दर से घट रहा है। लूप में प्रेरित धारा की दिशा और परिमाण निकालें यदि इसका प्रतिरोध 4.50mΩ हो।
05:40View SolutionA vector →A points vertically upward and →B oints towards north. The vector product →A×→B is
07:54View SolutionConsider Gauss's law
∮→E⋅→ds=qε0
Then, for the situation shown in figure at the Gaussian surface
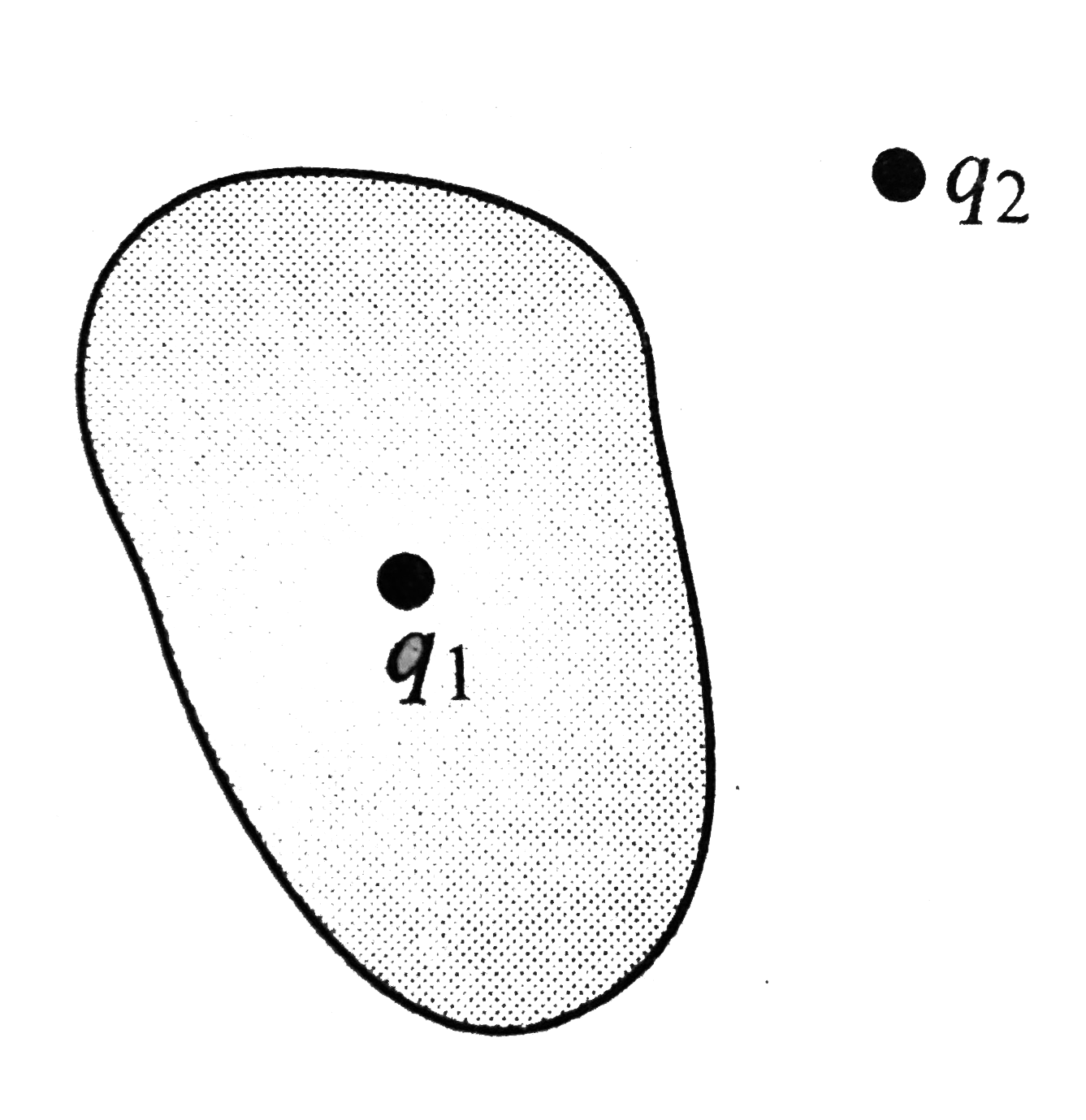 06:41View Solution
06:41View SolutionMaxwell's equation ∮→B⋅d→s=0 says
06:49View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
कौन - कौन से समीकरणों →E ओर →B के स्त्रोत प्रदर्शित करती है ओर कौन सी नहीं ? आवेश रहित होने की स्थिति में समीकरणों का क्या प्रारूप होगा ।07:37View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
कौन - कौन से समीकरणों →E ओर →B के स्त्रोत प्रदर्शित करती है ओर कौन सी नहीं ? आवेश रहित होने की स्थिति में समीकरणों का क्या प्रारूप होगा ।04:59View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
स्थिर विधुत व चुम्बकीय क्षत्रो के लिए मैक्सवेल सेमीकरणे लिखिये02:32View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
यदि चुम्बक का एक धुव होता तो कौन सी समीकरणों को परिवर्तित करना पड़ताView Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
चारो समीकरणों में कौन सी समीकरण यह प्रदर्शित करती है की चुम्बकीय क्षेत्र किसी से उत्सर्जित अथवा समाप्त किया जा सकता हैView Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
चारो समीकरणों में कोनसी समीकरण यह प्रदर्शित करती हो की स्थिर विधुत क्षेत्र की रेखाएं बंद लूप नहीं बनाती ?01:32View Solutionमैक्सवेल की सैमीकरणे व लारेंज बल का नियम दिया गया है -
(I)∮→E.D→A=q∈0
(ii)∮→B.D→A=0
(iii)∮→E.D→l=−ddt∫s→B.D→A
(iv)∮→B.d→l=μ0Ic+μ0∈0ddt∫s→E.d→A
लॉरेज बल =→F=q(→E+→v×→B)
इन सेमीकरणे से सम्बन्धित निम्न से उतर दो -
क्या उपरोक्त सेमीकरणे विभिन्न माध्यमों , परावैधुत , चालक व प्लाज्मा इत्यादि के लिए सही है।02:20View SolutionThe maxwells four equations are written as i. oint vec(E).vec(dS) = (q)/(epsilon_(0)) ii. oint vec(B).vec(dS) = 0 iii. oint vec(E ).vec(dl) = (d)/(dt) oint vec(B).vec(dS) iv. oint vec(B).vec(dl) = mu_(0) epsilon (d)/(dt) oint vec(E).vec(dS) The equations which have sources of vec(E ) and vec(B) are
View Solution

