A small block is resting on an inclined plane (co-efficient of friction μ>tanθ) as shown in the figure. The inclined plane is given a constant horizontal acceleration 'a' towards right.
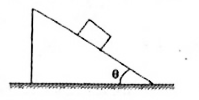
(a) Find the range of 'a' such that the bock does not slide on the plane.
(b) Find the value of 'a' such that the firction force between the block and the plane is zero.
The correct Answer is:0 to μ+tanθ1−μtanθ.g,a=gtanθ
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (Level-II & III)
18 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) (Level - 1)
50 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (Level-I)(True/False)
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Numerical Based Type
2 Videos
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?
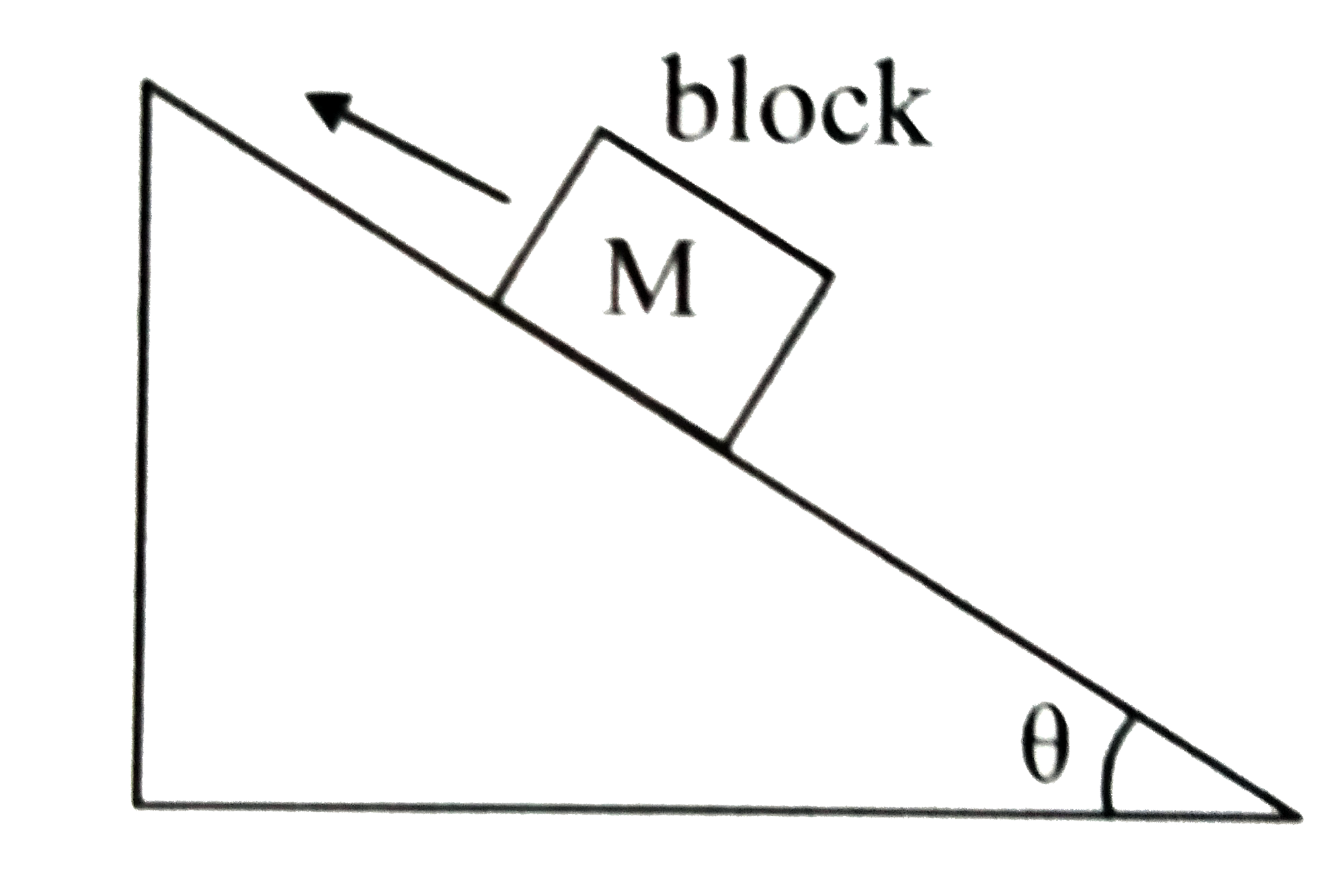
View Solution
Knowledge Check
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θIn if the inclined plane is not accelerating and the block is then sliding down the plane, force exerted by the block on the plane is:
AmgtanθBmgsinθCmgDnone of theseA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
A block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block
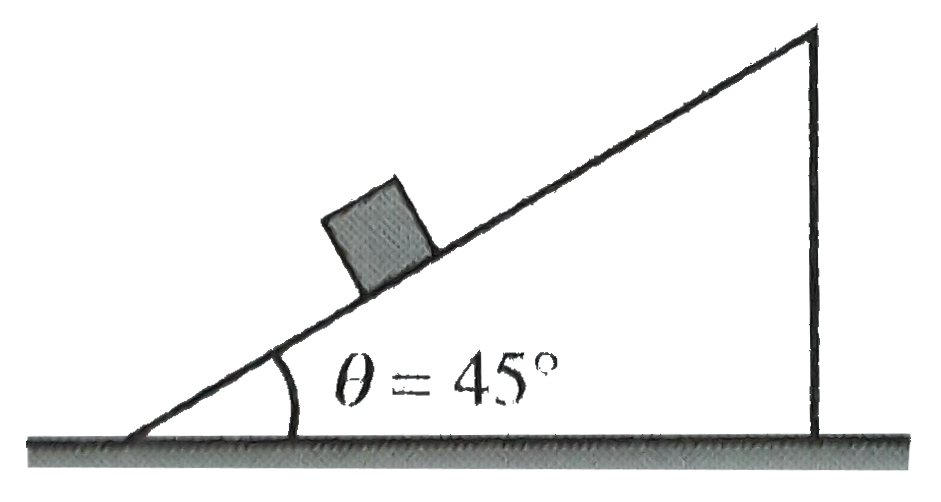
View SolutionA block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block

View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?

View SolutionA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
View SolutionA block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
View Solution
