The arrangement shown in the figure, the systme of masses m1,m2 and m3 is being pushed by a force F applied on m1 horizontally. In order to prevent the downwards slipping of m2 between m1 and m3 if coefficient of friction between m2 and m3 is μ and all the other surface are smooth, the minimum value of F :
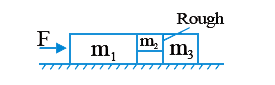
The correct Answer is:(m1+m2+m3)m2gμ m3 .
Step by step video, text & image solution for The arrangement shown in the figure, the systme of masses m_(1), m_(2) and m_(3) is being pushed by a force F applied on m_(1) horizontally. In order to prevent the downwards slipping of m_(2) between m_(1) and m_(3) if coefficient of friction between m_(2) and m_(3) is mu and all the other surface are smooth, the minimum value of F : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (Level-II & III)
18 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) (Level - 1)
50 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) (Level-I)(True/False)
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Numerical Based Type
2 Videos
Similar Questions
When force F applied on m2 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ… What should be the minimum value of F so that there is no relative motion between m1andm2
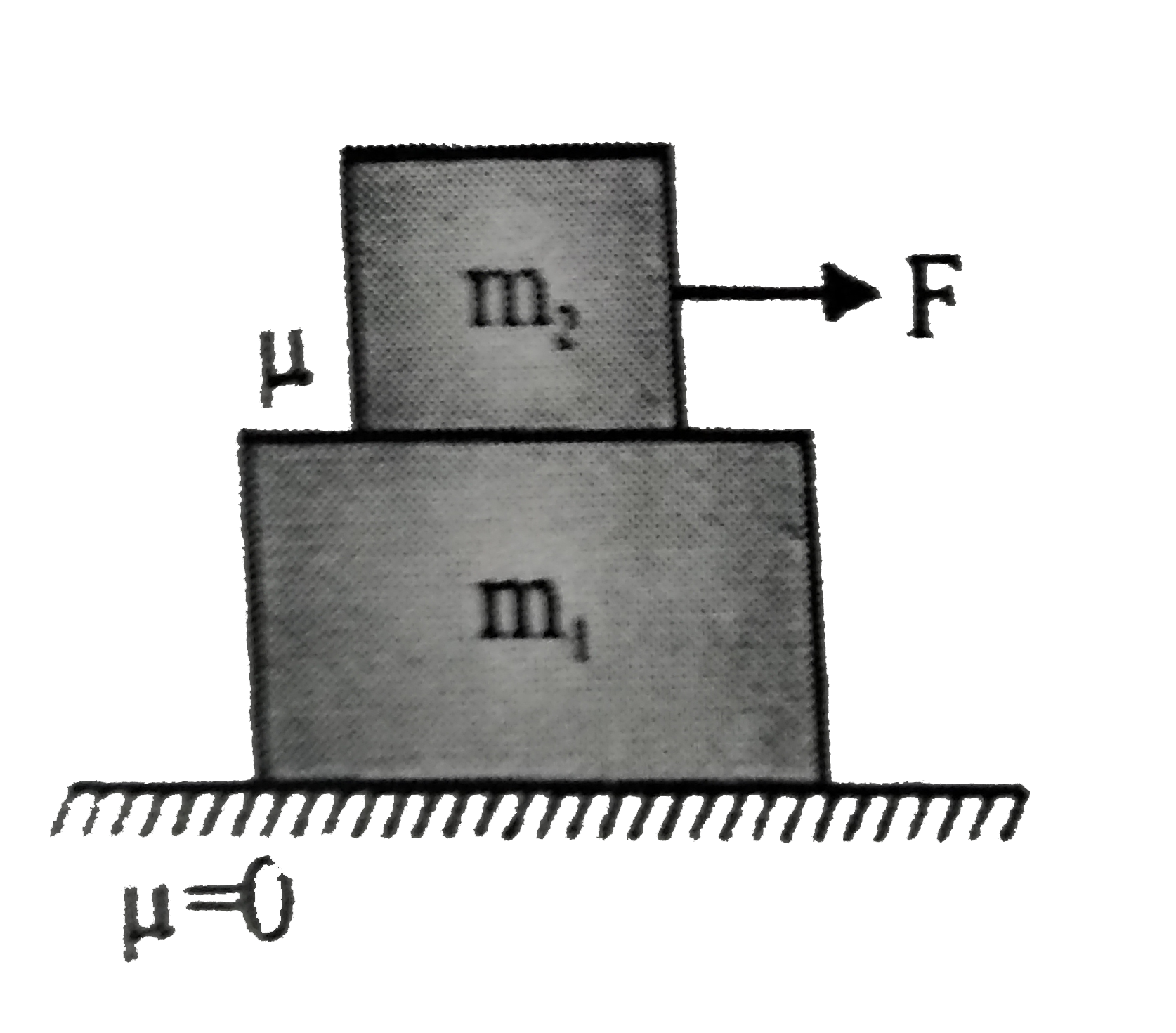
View SolutionWhen force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2

View Solution
Knowledge Check
In Fig. 7.150 , coefficient of friction between m2 and the horizontal surface is μ , minimum value of m so that the system has zero acceleration , is :
 Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2
Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2In the arrangement shown in figure, there is a friction force between the blocks of masses m and 2m. The mass of the suspended block is m. The block of mass m is stationary with respect to block of mass 2m. The minimum value of coefficient of friction between m and 2m is
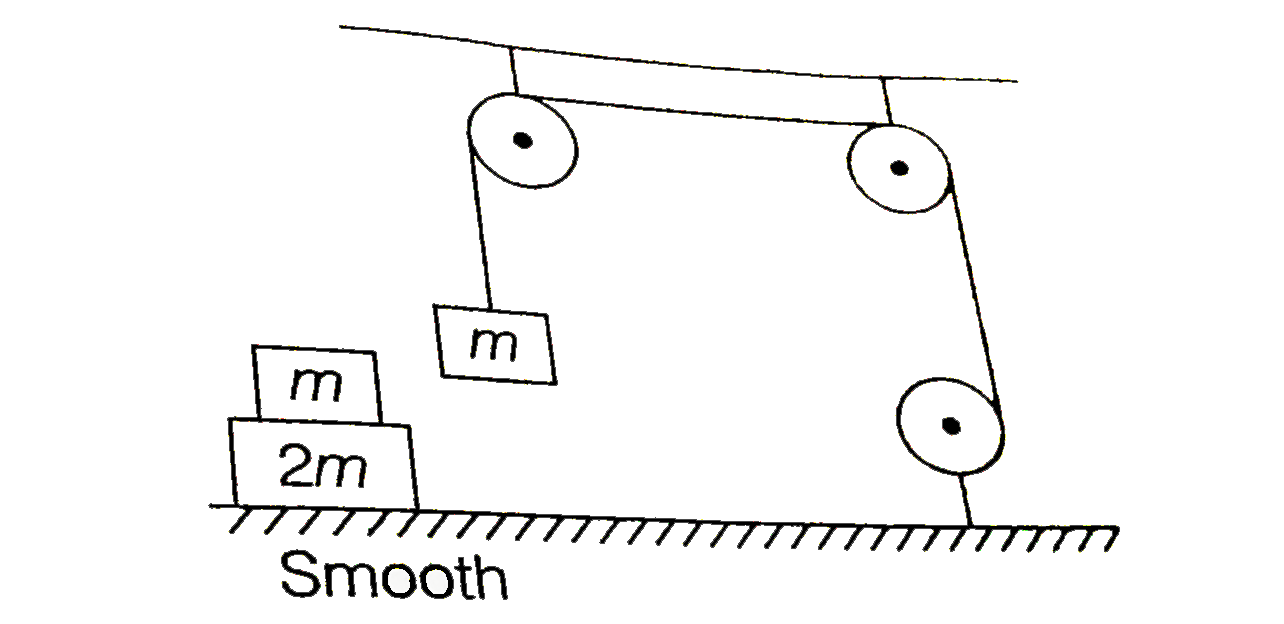 A12B1√2C14D13
A12B1√2C14D13In the figure shown m1=5kg,m2=10kg & friction coefficient between m1&m2 is μ=0.1 and ground is frictionless then :
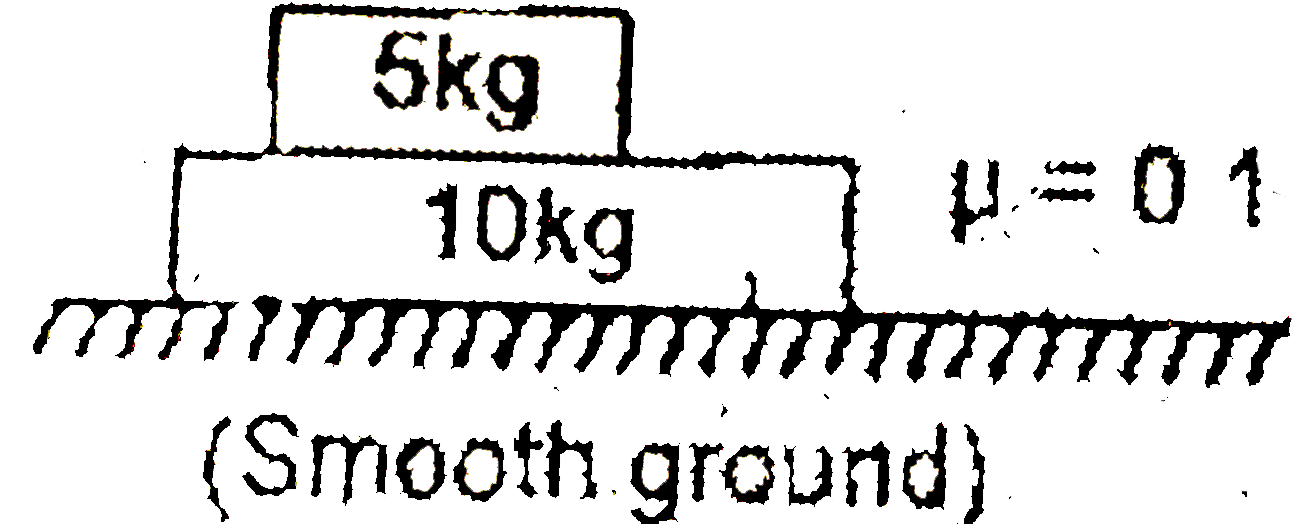 AIf a horizontal force F=20N is applied on m1 then the friction force acting on m2 is 5 N in the direction of FBMaximum amount of horizontal force that can be applied to m2 such that there is no relative motion between blocks is 15 NCIf a horizontal force F=20N is applied on m2 then friction force acting on m1 is 20/3 N in the direction of applied forceDMaximum amount of horizontal force that can be applied to m1 such that there is no relative motion between blocks is 8 N
AIf a horizontal force F=20N is applied on m1 then the friction force acting on m2 is 5 N in the direction of FBMaximum amount of horizontal force that can be applied to m2 such that there is no relative motion between blocks is 15 NCIf a horizontal force F=20N is applied on m2 then friction force acting on m1 is 20/3 N in the direction of applied forceDMaximum amount of horizontal force that can be applied to m1 such that there is no relative motion between blocks is 8 N
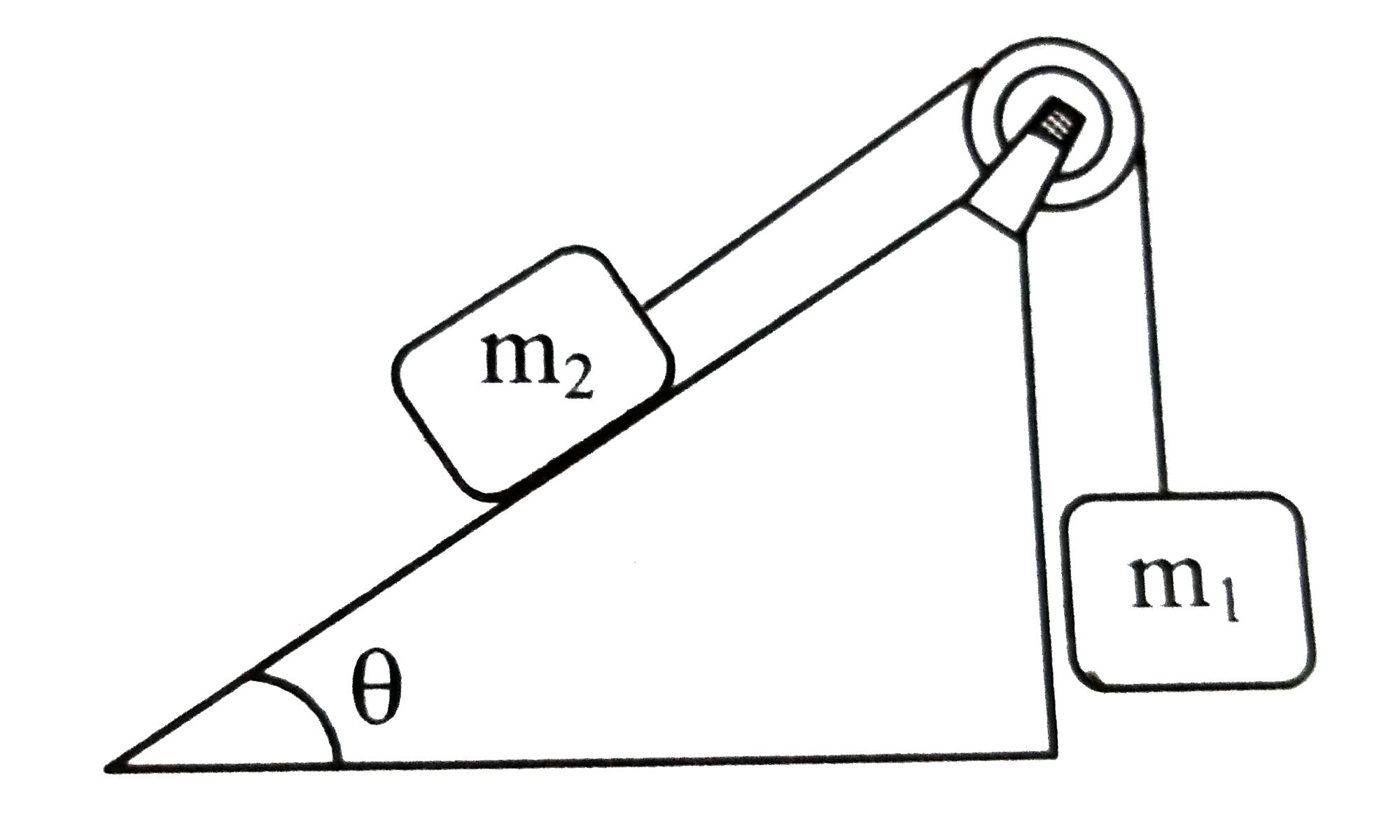
The coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
View SolutionWhen force F applied on m1 and surface. Is μ1 and the coefficient of friction between m1andm2 is μ2. What should be the minimum value of F so that there is no relative motion between m1andm2.

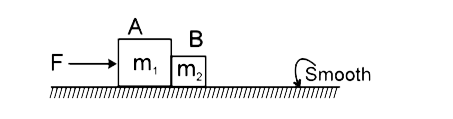
View SolutionA force F is applied horizontally on mass m1 as shown in figure. Find the contact force between m1 and m2
View SolutionWhat force F must be applied so that m1 and m2 are at rest on m3 in
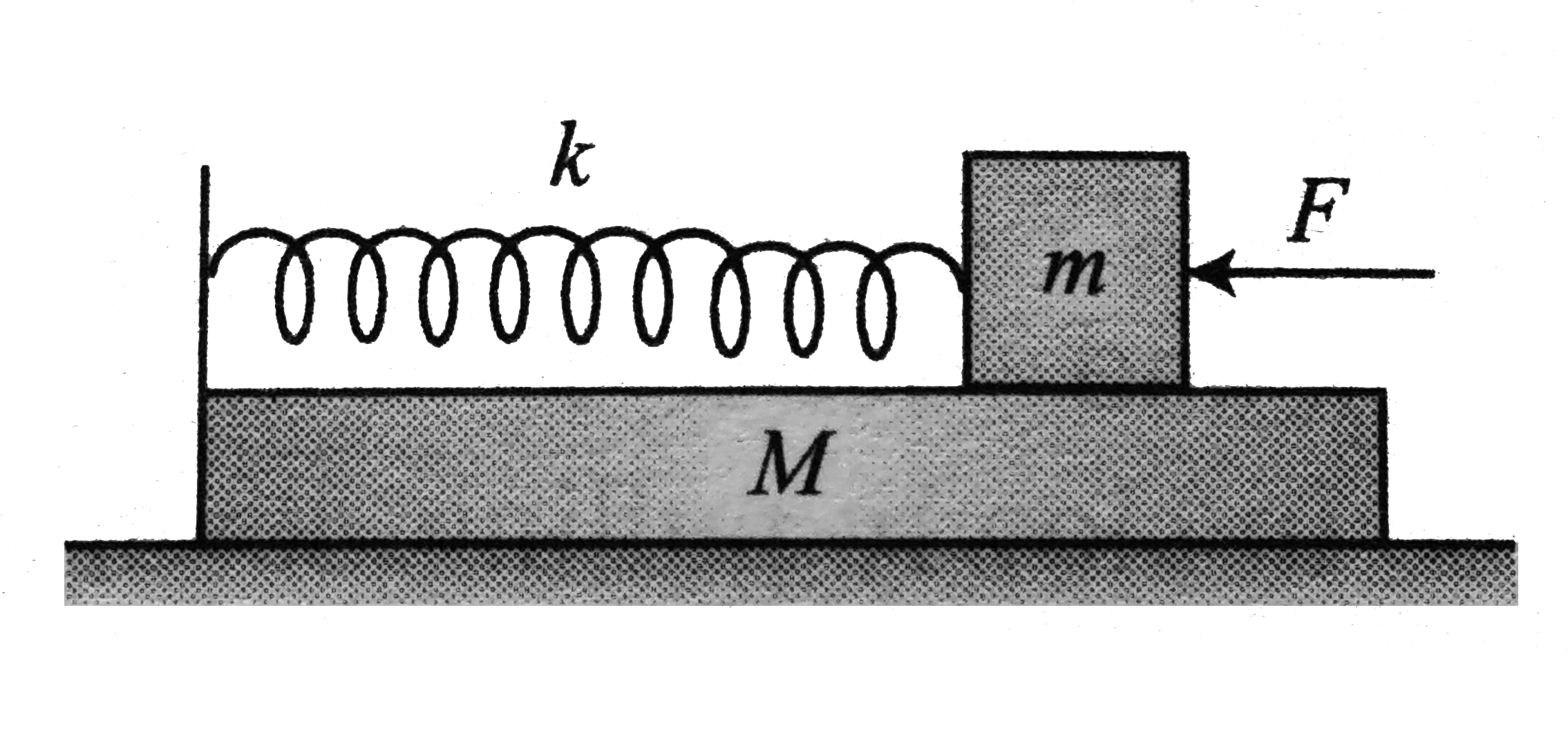
View SolutionA constant force F pushes the block m till the wedge M starts sliding. If the stiffness of the light spring connecting M and m is K, coefficient of friction between block and wedge is μ1 and between the wedge and ground is μ2, find the value of the force F
View Solution
