A ring of mass m and radius a is connected to an inextensible string which passes over a frictionless pulley. The other end of string is connected to upper end of a massless spring of spring constant k. The lower end of the spring is fixed. The ring can rotate in the vertical plane about hinge without any friction. If horizontal position of ring is equilibrium position then find time period of small in oscillations of the ring.
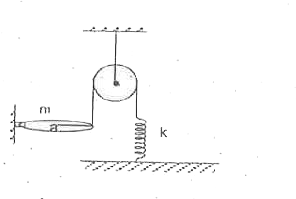
When displacement of the ring is θ, then extension in spring =(2aθ+x0)
Energy of system
E=12k(2aθ+x0)2−mgaθ+12l(dθdt)2
E=12k(2aθ+x0)2−mgaθ+12(12ma2+ma2)(dθdt)2
⇒dEdt=k(2aθ+x0)2adθdt−mgadθdt+32ma2(dθdt)d2θdt2
As dEdt=0,k(2aθ+x0)2a−mga=−32ma2d2θdt2
4akθ+2akx0−mga=−32ma2d2θdt2
∴83kmθ=−d2θdt2
∴ω=√8k3m
∴T=2π√3m8k
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Objective)
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - COMPREHENSION
17 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
Two masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View SolutionA uniform semicircular ring of mass m and radius r is hinged at end A so that it can rotate freely about end A in the vertical plane as shown in the figure. Calculate angle made by line AB with vertical in equilibrium position and time period of small oscillation of ring.

View Solution
Knowledge Check
Two masses m and m (m>m) are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of centre of mass is
A(m1−m2m1+m2)2gBm1−m2m1+m2gCm1+m2m1−m2gDZeroA Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
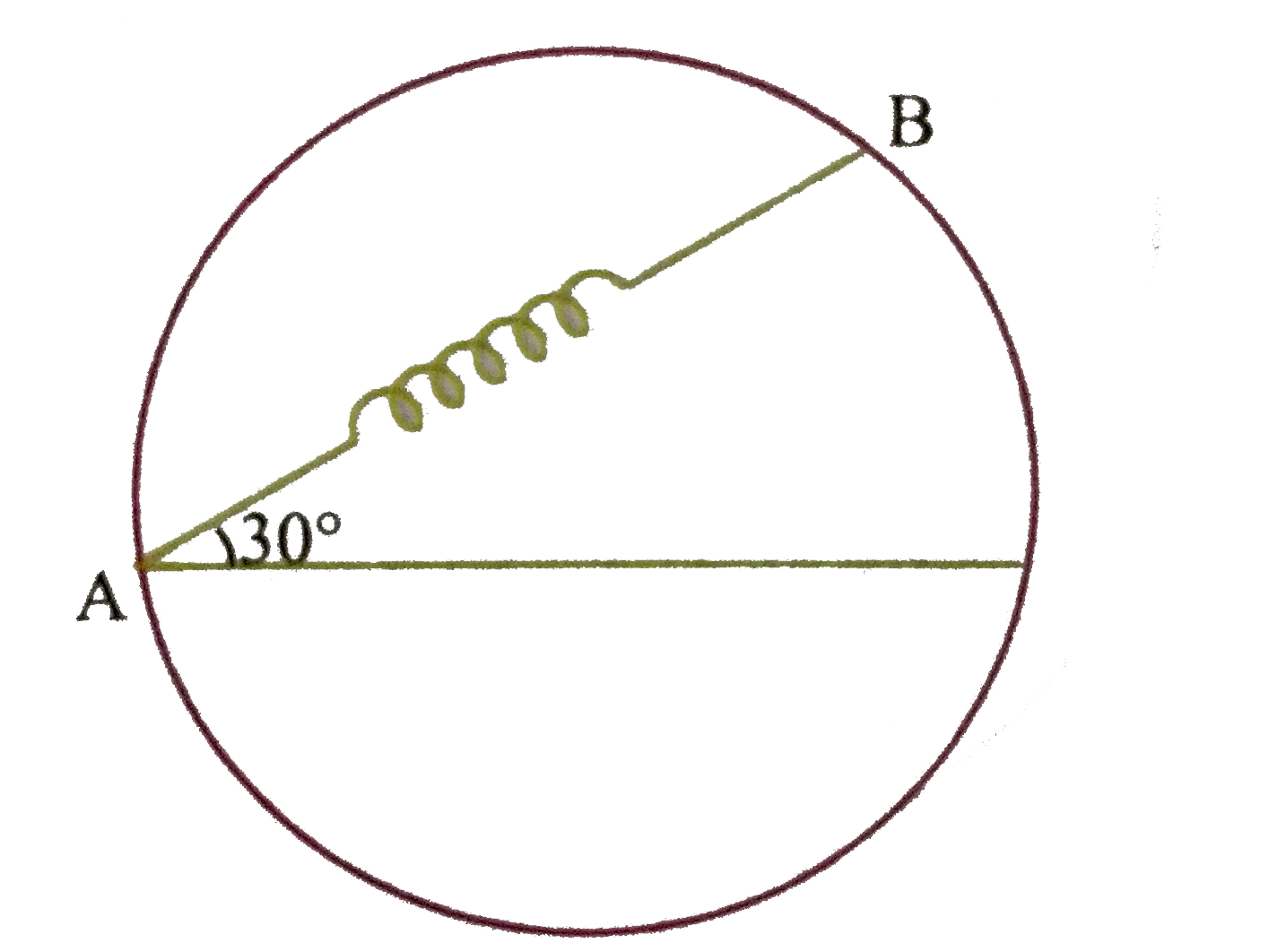 AThe normal reaction at 'B' just after the bead is released to move is:3√3mg2BThe tangential acceleration of the bead just after it is released to move is :g/2CThe normal reaction at 'B' just after the bead is released to move is :3mg2DJust after the bead is released to move the normal acceleration and Tangential acceleration are numerically equal.
AThe normal reaction at 'B' just after the bead is released to move is:3√3mg2BThe tangential acceleration of the bead just after it is released to move is :g/2CThe normal reaction at 'B' just after the bead is released to move is :3mg2DJust after the bead is released to move the normal acceleration and Tangential acceleration are numerically equal.A block of mass 2 m hangs by an inextensible light string that passes over a smooth pulley. Another mass m hangs from the other end of the string and is connected to a vertical massless spring. The system is stationary. Just after the string is cut, the accelerations of m and 2m, respectively, are -
 A0,0B0,g↓Cg2⏐⏐ ⏐↓g⏐⏐ ⏐↓D2g↓,g↓
A0,0B0,g↓Cg2⏐⏐ ⏐↓g⏐⏐ ⏐↓D2g↓,g↓
A uniform semicircular ring of mass m and radius r is hinged at end A so that it can rotate freely about end A in the vertical plane as shown in the figure. Calculate angle made by line AB with vertical in equilibrium position and time period of small oscillation of ring.

View SolutionA light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

View SolutionA light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

View Solution
A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionA 10 kg mass is connected at one end of a massless spring with force constant k = 1000 N/m, keeping other end fixed in a horizontal plane as shown in the fig. 15.6
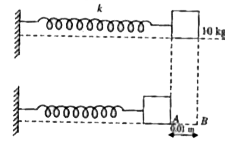 If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is
If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is
View Solution
