Find the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.

Let the bar be rotated through a small angle θ. The restoring torque of the force mg k1xandk2x about O can be given as
τ=−[mg(l)2sinθ+k1x(lcosθ)+k2x(lcosθ)]
⇒τ=−[(k1+k2)l×cosθ+mg(l)2sinθ]
since, θ is small sin≅θ,x=lθ&cosθ≅1
Putting k1+k2=k we obtain
τ=−[kl2+mg(l)2]θ
⇒lα=−(kl2+mg(l)2)θ
⇒ωosc=
⎷(kl2+mg(l/2)(ml2/3))=√3km+3g2l
n=12π√3km+3g2l

Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Objective)
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - COMPREHENSION
17 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
Find the frequency of small oscillatinos of a thin uniform vertical rod of mass m and length l hinged at the point O (figure). The combined stiffness fo the springs is equal to x. The mass of the springs is negligible.
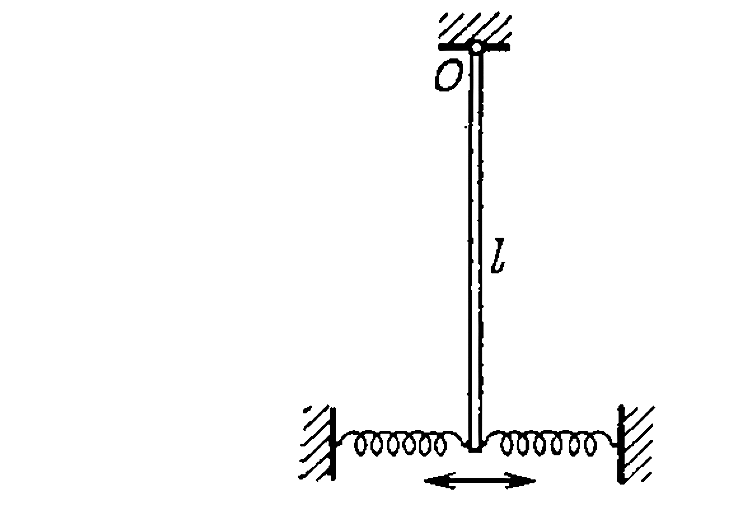
View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
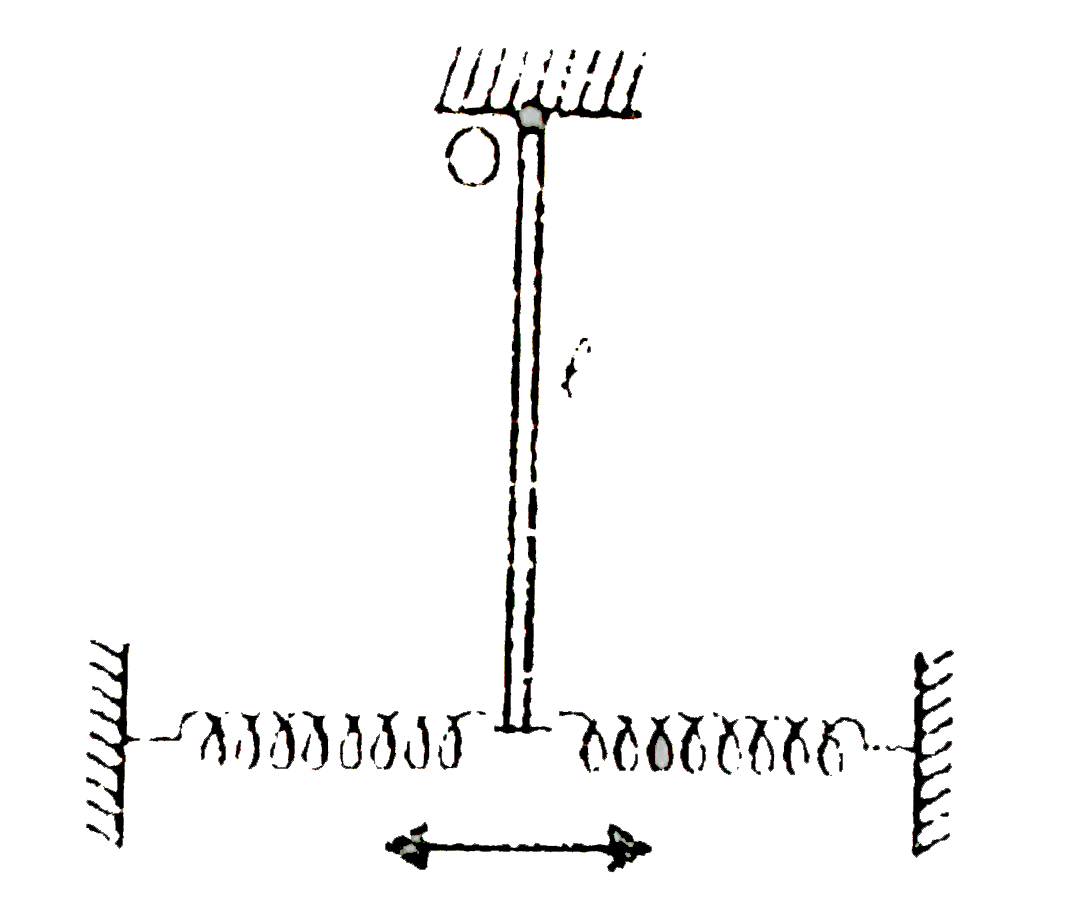
View Solution
Knowledge Check
Moment of inertia of a thin rod of mass 'M' and length 'L' perpendicular to rod at mid point is
AMl22,BMl23CMl212DNone of these
A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. The frequency of small oscillation is .A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l
If the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
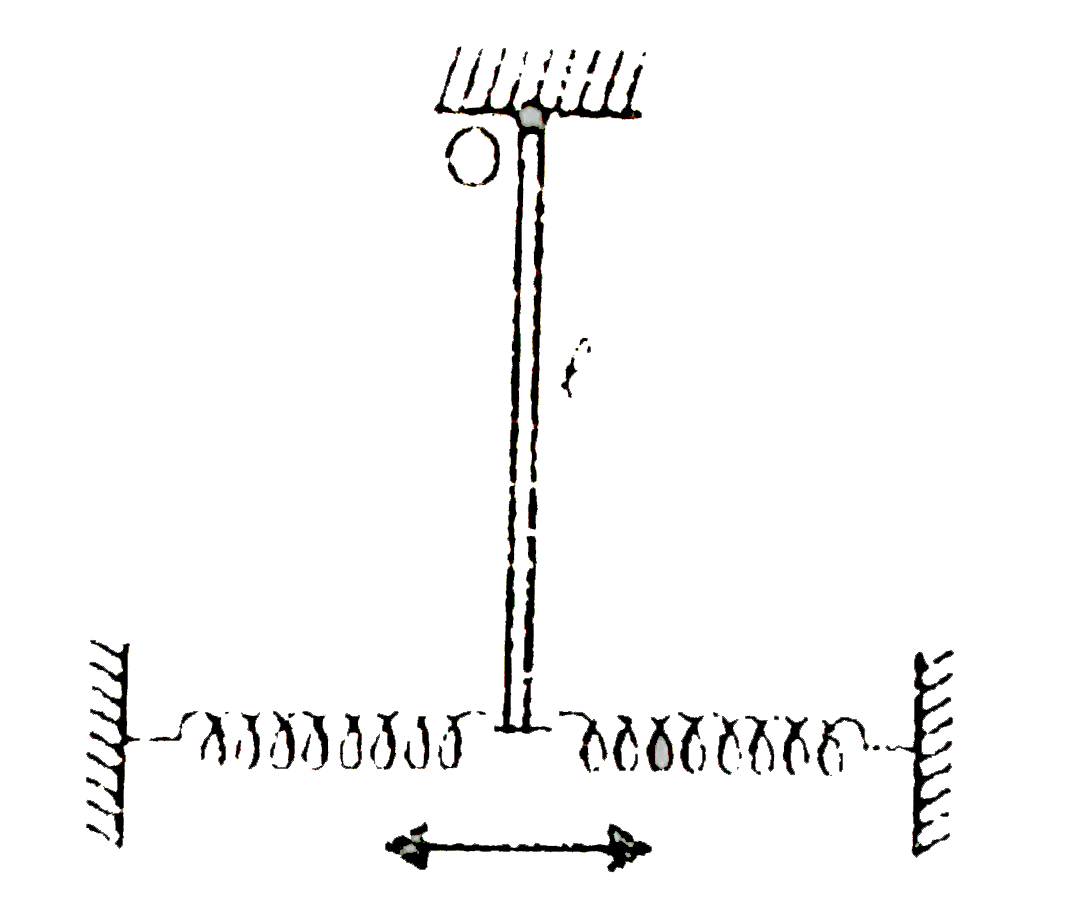
View SolutionFind the M.I. of thin uniform rod of mass M and length L about the axis as shown.

View SolutionFind the period of small oscillations of a uniform rod with length l , pivoted at one end.
View SolutionShow that the centre of mass of uniform rod of mass M and length L lies at the middle point of the rod.
View SolutionFind the gravitational potential energy of a system consisting of a uniform rod AB of mass M, length l and a point mass m as shown in figure.
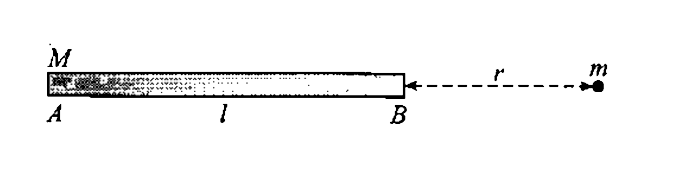
View SolutionFind the gravitational potential energy of system consisting of uniform rod AB of mass M, length l and a point mass m as shown in figure.

View Solution
