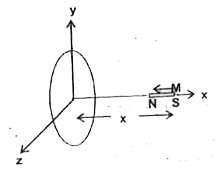
An infinitesimal bar magnet of dipole moment $M$ is pointing and moving with speed $v$ in the $x$ -direction. A closed circular conducting loop of radius a and negligible self-inductance lies in the $y - z$ plane with its centre at $x = 0$ and its axis coinciding with $x$ -axis. find the force opposing the motion of the magnet, if the resistance of the loop is $R$ . Assume that the distance $x$ of the magnet from the centre of the loop is much greater than a .

Video Solution

Text Solution

Verified by Experts

A bar magnet can be thought of a current carrying coil of dipole moment M. The magnetic field of a current carrying coil at a distance x on its axis (x $> >$ radius of the coil ) can be given as
$B = \frac{μ_{0} (2 M)}{4 π X^{3}} = \frac{μ_{0} M}{2 π X^{3}}$
$\Rightarrow$ The flux linked with the given loop
$ϕ$ = B . (area of the loop )
$\Rightarrow ϕ = B (π a^{2}) = \frac{μ_{0} M a^{2}}{2 x^{3}}$
emf induced in the loop
$E = - \frac{d ϕ}{d t} = - \frac{d}{d t} [\frac{μ_{0} M a^{2}}{2 x^{3}}]$
$\Rightarrow E = \frac{3 μ_{0} M a^{2}}{2 x^{4}} \frac{d x}{d t} = \frac{3 μ_{0} M a^{2}}{2 x^{4}} v$
The induced current in the loop =i = $\frac{E}{R} = \frac{3 μ_{0} M a^{2} v}{2 R x^{4}}$
The induced dipole moment of the loop = M =I ( $π a^{2})$
$\Rightarrow M . = \frac{3 μ_{0} M a^{2} v}{2 R x^{4}} (π a^{2})$
The force of interaction between two dipoles of dipole moment pointing along the line joining their centres can be written as
$F = \frac{3 μ_{0} M M}{2 π x^{4}}$ where x= separation between them.
Putting the values M we obtain
$F = \frac{0 μ_{0}^{2} M^{2} a^{4}}{4 x^{8} R}$ v

Updated on:21/07/2023