A magnetic field B=B0(y/a)(^)k is into the paper in the +z direction, B0 and a are positive constants. A square loop EFGH of side a, mass m and resistance R, in x-y plane, starts falling under the influence of gravity see figure. Note the direction of x and y axis in figure.
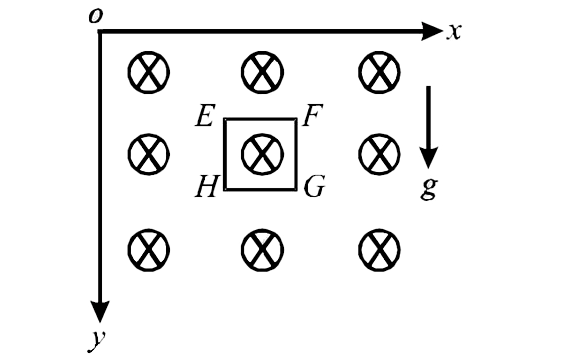
Find
(a) the induced current in the loop and indicate its direction.
(b) the total Lorentz force acting on the loop and indicate its direction, and
(c) an expression for the speed of the loop, v(t) and its terminal value.
(a) Let v = velocity of the loop at any time t.
⇒ The induced emf between E & F.
=e1=B1av=B0yaav=B0yv
The induced emf between H and G
=e1=B2av=B0(y+a)aav=B0(y+a)
⇒ The net emf =e=ez−e1=B0av
⇒ The induced current =i=−eR=B0avR anticlockwise because
ez>e1
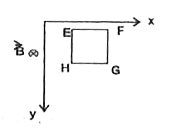
(b ) The Lorentz force on EF & HG are given as
F1=B0Yaia=B0yi&F2=B0(Y+a)aia=B0(y+a)i
⇒F=F2−F1=B0 a i along negative -Y axis
⇒F=−B0aiˆy
⇒F=−B20a2vR
( c) Fnet=mg−B20a2vRˆy
⇒mdvdt=mg−B20a2vR
⇒∫v0dv(mg−B20a2vR)=∫10dtm
Evaluating the integration and rearranging the terms we get
v=mgRB20a2⎡⎢⎣1−e−(B20a21mR)⎤⎥⎦
When t→∞,v→Vterminal
⇒Vterminal=mgRB20a2.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SOLVED PROBLEMS ( OBJECTIVE)15videos
ELECTROMAGNETIC INDUCTION
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Comprehension Based Type Comprehension -I3videos
ELECTROMAGNETIC INDUCTION
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
- BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Assignment Problems (Objective) Level-II15videos
ELASTICITY AND WAVES
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTION AND AC CURRENTEXERCISE - Example15videos
ELECTROMAGNETIC INDUCTION AND AC CURRENT
Similar Questions
Shown in the figure is a circular loop of radius r and resistance R. A variable magnetic field of induction B=B0e−t is established inside the coil. If the key (K) is closed, the electric power developed right after closing the switch is equal to:-
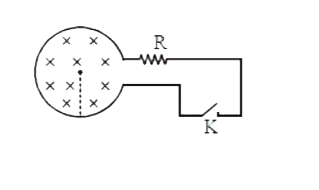20:35View SolutionTwo parallel vertical metallic rails AB and CD are separated by 1m. They are connected at the two ends by resistances R1 and R2 as shown in the figure. A horizontal metallic bar l of mass 0.2kg slides without friction, vertically down the rails under the action of gravity. There is a uniform horizontal magnetic field of 0.6T perpendicular to the plane of the rails. It is observed that when the terminal velocity is attained, the powers dissipated in R1 and R2 are 0.76W and 1.2W respectively (g=9.8m/s2)
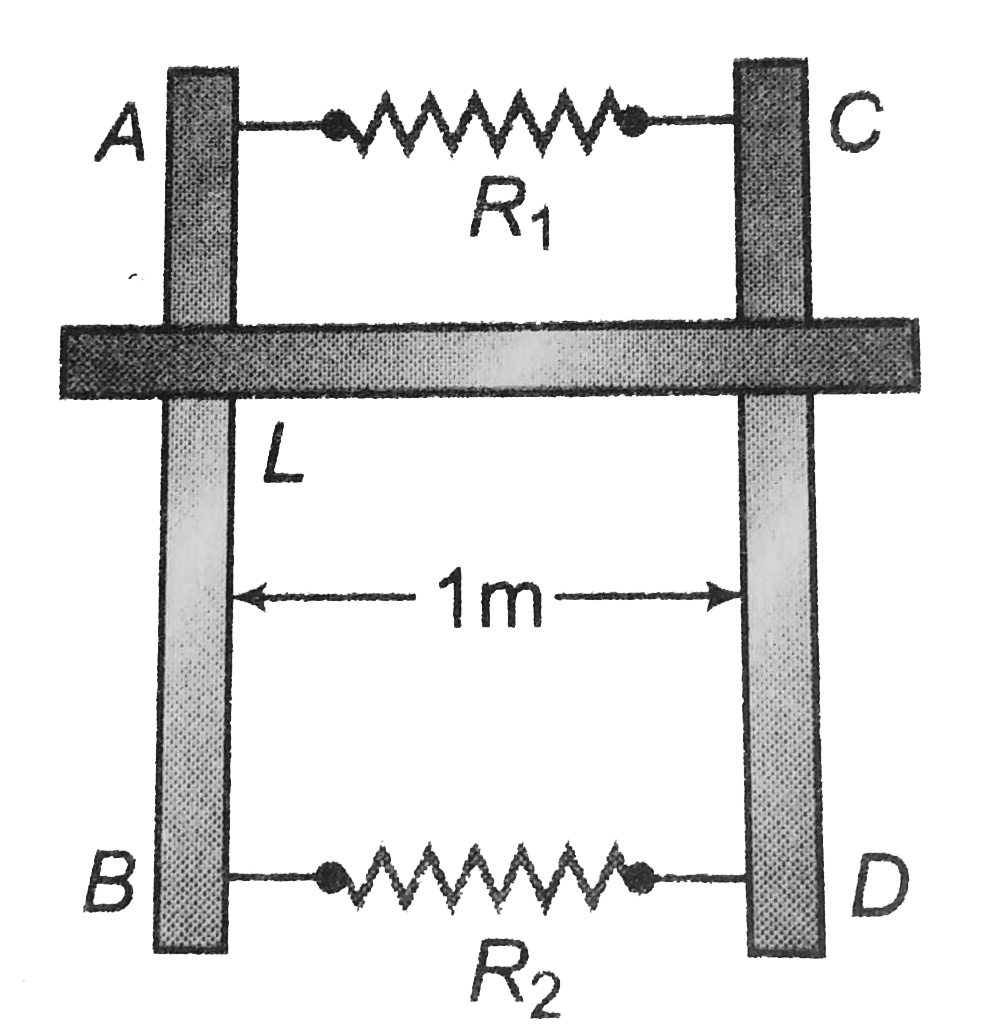
The terminal velocity fo the bar L will be04:29View SolutionReferring to the previous illustration what will be the induced e.m.f at any instant if the loop is rotated an axis passing through the centre and parallel to the length ?
02:28View SolutionWhen does an elastic metal rod change its length?
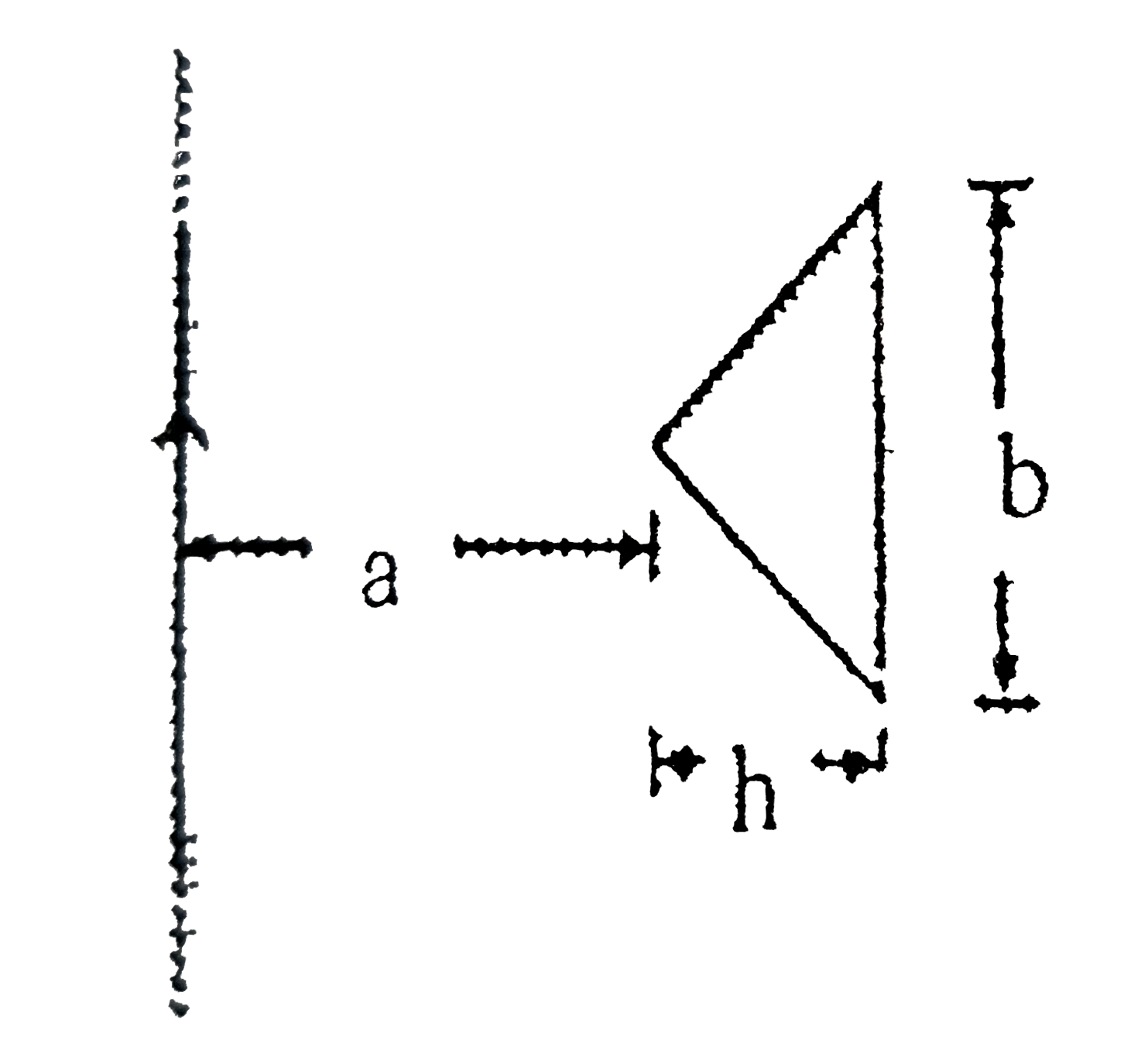
View SolutionA very long staright conductor and an isoceles triangular conductor lie in a plane and separated from each other as shown in the figure.
Given a=10cm, b=20cm and h=10cm
(a) Find their coefficeint of mutual induction.
(b) If current in the staright wire is increasing at a rate of 2A/s , find the direction and magnitude of current in the triangular wire. [Diameter of the wire crosss-section d=1mm, resistivity of the wire, ρ=1.8×10−8Ω−m]
03:36View SolutionA magnetic field B=B0(y/a)(^)k is into the paper in the +z direction, B0 and a are positive constants. A square loop EFGH of side a, mass m and resistance R, in x-y plane, starts falling under the influence of gravity see figure. Note the direction of x and y axis in figure.
Find
(a) the induced current in the loop and indicate its direction.
(b) the total Lorentz force acting on the loop and indicate its direction, and
(c) an expression for the speed of the loop, v(t) and its terminal value.08:05View SolutionIf the work required to move the conductor shown in figure, one full turn in the positive direction at a rotational frequency N revolutions per minute, if →B=B0ˆar(B0 is positive constant and ˆar is a unit vector in radial direciton ), is yπrB0il. Then y is .
15:45View SolutionThe magnetic field in a region is given by vec(B)=B_(0)(1+(x)/(a))hat(k) . A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity vec(V)=V_(0)hat(i) . The emf induced in the loop is
04:54View SolutionThe magnetic field I nan reigion is given by B=B0XaK. A Squrae edges along the x and y axis. The loop is moved with a constant velocity . The emf induced in the loop is
04:00View SolutionA current carrying circular loop of radius R is placed in a uniform magnetic field B_(0) Tesla in x-y plane as shown in figure. The loop carries a current i = 1A in the direction shown. Find the torqure acting on the loop
22:15View Solutionएक चुंबकीय क्षेत्र →B=(B0ya)ˆk कागज के तल के लंबवत अंदर की ओर +z अक्ष के अनुरेख दिष्ट हैं । B0 तथा a धनात्मक नियतांक हैं । PQRS एक वर्गाकार लूप हैं जिसकी भुजा = a , द्रव्यमान = m तथा प्रतिरोध = r हैं । यह लूप गुरुत्व के अधीन X-Y तल के समांतर विराम से नीचे की ओर गिरता हैं ।
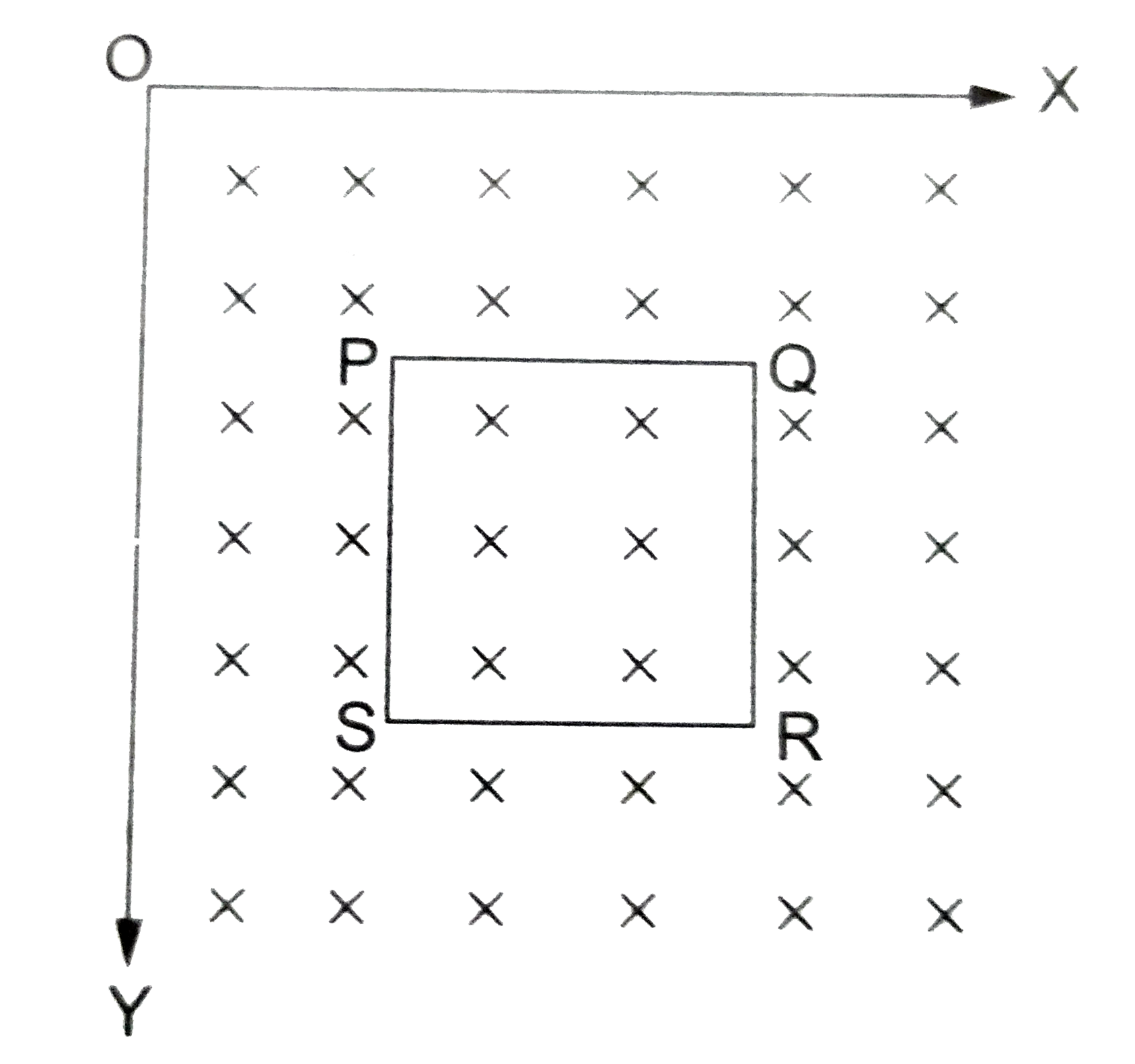
गति के क्रम में जब लूप की चाल v हो तब लूप में प्रेरित धारा का मान तथा दिशा हैंView Solutionएक चुंबकीय क्षेत्र →B=(B0ya)ˆk कागज के तल के लंबवत अंदर की ओर +z अक्ष के अनुरेख दिष्ट हैं । B0 तथा a धनात्मक नियतांक हैं । PQRS एक वर्गाकार लूप हैं जिसकी भुजा = a , द्रव्यमान = m तथा प्रतिरोध = r हैं । यह लूप गुरुत्व के अधीन X-Y तल के समांतर विराम से नीचे की ओर गिरता हैं ।
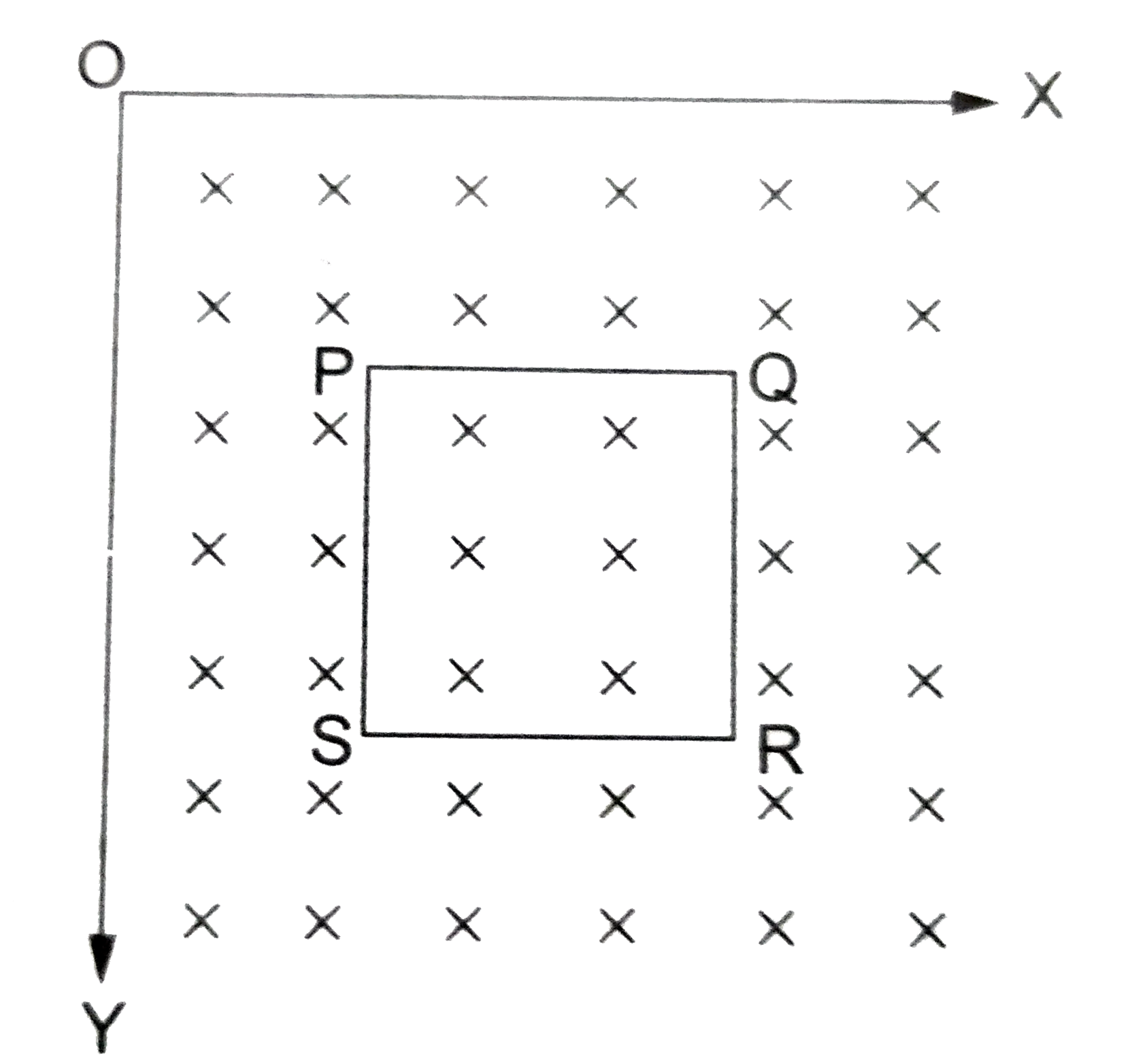
गति के क्रम में जब लूप की चाल v हो तब लूप पर आरोपित नेट लोरेंट्ज़ बल का परिमाण एवं दिशा है02:21View Solutionएक चुंबकीय क्षेत्र →B=(B0ya)ˆk कागज के तल के लंबवत अंदर की ओर +z अक्ष के अनुरेख दिष्ट हैं । B0 तथा a धनात्मक नियतांक हैं । PQRS एक वर्गाकार लूप हैं जिसकी भुजा = a , द्रव्यमान = m तथा प्रतिरोध = r हैं । यह लूप गुरुत्व के अधीन X-Y तल के समांतर विराम से नीचे की ओर गिरता हैं ।
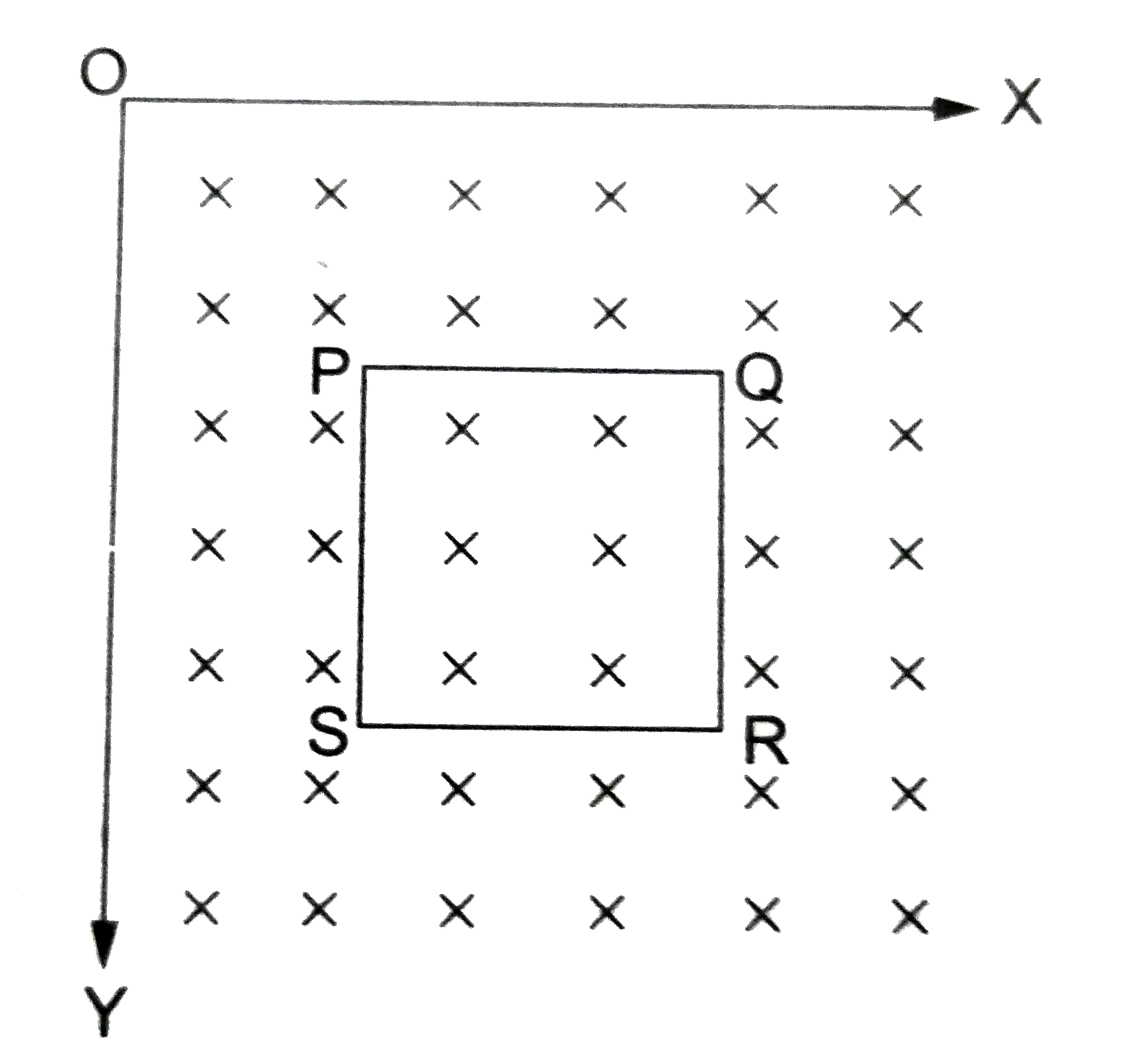
गुरुत्व की अनुपस्थिति में यदि लूप एकसमान वेग v से xy-तल में x-अक्ष के समांतर गतिशील हो तब लूप में प्रेरित धारा का मान तथा दिशा हैं04:31View SolutionA square loop EFGH of side a, mass m and total resistance R is falling under gravity in a region of transverse non - uniform magnetic field given by B=By0a =, where B0 is a positive constant and y is the position of side EF of the loop. If at some instant the speed of the loop is v, then the total Lorentz acting on the loop is
03:42View Solutionएक चुम्बकीय क्षेत्र B=(B0y/a)ˆk कागज के तल के लम्बवत् नीचे की ओर +z दिशा में है। B, Ra धन नियतांक हैं। एक वर्गाकार लूप EFGH जिसकी भुजा a, द्रव्यमान m तथा प्रतिरोध R है, X-y तल में गुरुत्व के अन्तर्गत गिरना प्रारम्भ करता है। चित्र में x तथा y-अक्षों की दिशाओं का ध्यान रखते हुए ज्ञात कीजिए।
(a) लूप में प्रेरित धारा तथा इसकी दिशा
(b) लूप पर कार्य करने वाला लॉरेन्ज बल तथा उसकी दिशा,
(c) लूप की चाल v(t) का व्यंजक तथा चाल का सीमान्त मान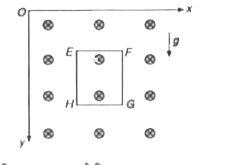
05:21View SolutionA rectangular, a square, a circular and an elliptical loop, all in the x-y plane, are moving out of a uniform magnetic field with a constant velocity vcev = v_(0)hati . The magnetic field is directed along the negative z-axis direction. The induced emf, during the passage of these loops, out of the field region, will not remain constant for
05:32View Solution