A small object is placed at the centre of the bottom of a cylindrical vessel of radius 3 cm and height 4 cm filled completely with water. Consider the ray leaving the vessel through a corner. Suppose this ray and the ray along the axis of the vessel are used to trace the image. Find the apparent depth of the image and the ratio of real depth to the apparent depth under the assumptions taken. Refractive index -of water = 1-33.
The correct Answer is:A, B, C
To solve the problem step by step, we will analyze the situation involving the cylindrical vessel filled with water and the object placed at the bottom.
Step 1: Understand the Setup
We have a cylindrical vessel with a radius of 3 cm and a height of 4 cm filled with water. An object is placed at the center of the bottom of the vessel.
Step 2: Identify the Rays
Two rays are considered:
1. A ray that leaves the object and exits the vessel through a corner.
2. A ray that travels directly along the axis of the vessel.
Step 3: Determine the Real Depth
The real depth (d) of the object from the surface of the water is given as 4 cm (the height of the vessel).
Step 4: Apply Snell's Law
Using Snell's law, we can relate the angles of incidence (I) and refraction (R) as follows:
sinIsinR=n1n2
where n1 is the refractive index of air (approximately 1) and n2 is the refractive index of water (1.33).
Step 5: Calculate Sine of Angles
To find the angle of incidence (I), we can use the geometry of the triangle formed by the radius and the height:
- The radius of the vessel is 3 cm, and the height is 4 cm.
- We can find the hypotenuse using the Pythagorean theorem:
Hypotenuse=√(32+42)=√9+16=5 cm
- Therefore,
sinI=oppositehypotenuse=35
Step 6: Substitute into Snell's Law
Using Snell's law:
3/5sinR=11.33
Thus,
sinR=3/51.33=35×1.33=36.65≈0.451
Step 7: Calculate Apparent Depth
Using the relationship between the angles and the geometry of the situation, we can express the apparent depth (x):
tanR=3x
From the triangle, we know:
tanR=sinRcosR
Using the identity sin2R+cos2R=1, we can find cosR and hence calculate tanR.
Step 8: Find x
We can equate:
tanR=3xandtanR=43
Thus,
43=3x
Cross-multiplying gives:
4x=9⟹x=94=2.25 cm
Step 9: Calculate the Ratio of Real Depth to Apparent Depth
The ratio of real depth to apparent depth is:
Ratio=Real DepthApparent Depth=42.25≈1.78
Final Answers
1. The apparent depth (x) is 2.25 cm.
2. The ratio of real depth to apparent depth is approximately 1.78.
We have a cylindrical vessel with a radius of 3 cm and a height of 4 cm filled with water. An object is placed at the center of the bottom of the vessel.
Two rays are considered:
1. A ray that leaves the object and exits the vessel through a corner.
2. A ray that travels directly along the axis of the vessel.
The real depth (d) of the object from the surface of the water is given as 4 cm (the height of the vessel).
Using Snell's law, we can relate the angles of incidence (I) and refraction (R) as follows:
sinIsinR=n1n2
where n1 is the refractive index of air (approximately 1) and n2 is the refractive index of water (1.33).
To find the angle of incidence (I), we can use the geometry of the triangle formed by the radius and the height:
- The radius of the vessel is 3 cm, and the height is 4 cm.
- We can find the hypotenuse using the Pythagorean theorem:
Hypotenuse=√(32+42)=√9+16=5 cm
- Therefore,
sinI=oppositehypotenuse=35
Using Snell's law:
3/5sinR=11.33
Thus,
sinR=3/51.33=35×1.33=36.65≈0.451
Using the relationship between the angles and the geometry of the situation, we can express the apparent depth (x):
tanR=3x
From the triangle, we know:
tanR=sinRcosR
Using the identity sin2R+cos2R=1, we can find cosR and hence calculate tanR.
We can equate:
tanR=3xandtanR=43
Thus,
43=3x
Cross-multiplying gives:
4x=9⟹x=94=2.25 cm
The ratio of real depth to apparent depth is:
Ratio=Real DepthApparent Depth=42.25≈1.78
1. The apparent depth (x) is 2.25 cm.
2. The ratio of real depth to apparent depth is approximately 1.78.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE
9 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
The circumference of the base of a cylindrical vessel is 132 cm and its height is 25cm. How many litres of water can it hold?
View SolutionThe apparent depth of an object O from AB is
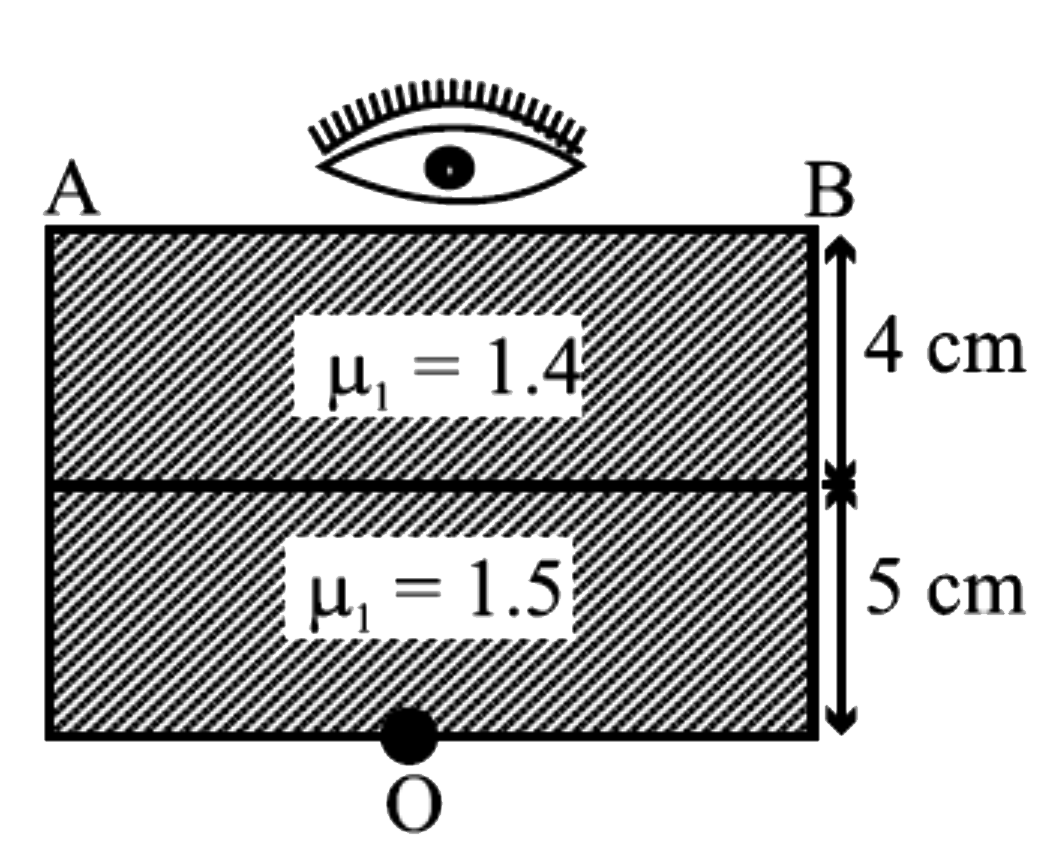
View SolutionIn Fig. , find the apparent depth of the object seen below surface AB.

View SolutionA charge q is placed at the centre of the open end of a cylindrical vessel . The flux of the electric field through the surface of the vessel is

View SolutionThe bottom of a cylindrical vessel has a circlular hole of radius r and at depth h below the water] level. If the diameter of the vessel is D, the find then speed with which the water level in the] vessel drops.
View SolutionThere is some water in a cylindrical vessel of radus 6 cm a sphere of radus 2 cm is dropped in to the vessel .Find the increase in the height of water surface.
View SolutionProve that
Refractive index=real depthapparent depth
View SolutionA conical vessel whose internal radius is 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height to which the water rises.
View SolutionA conical vessel whose internal radius is 5 cm and height 24cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10cms. Find the height to which the water rises.
View SolutionA conical vessel whose internal radius is 5 cm and height 24cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10cms. Find the height to which the water rises.
View Solution
