A smooth hemisphere is kept fixed on a horizontal floor . A small block f mass m is kept on the tip of hemisphere . Block is slightly pushed and it is found that block leaves contact with the spherical surface when radius through the block makes and angle θ with the vartical . Calculate θ .
To solve the problem of finding the angle θ at which the block leaves contact with the hemisphere, we will follow these steps:
Step 1: Understand the Forces Acting on the Block
When the block is at an angle θ with the vertical, two forces act on it:
- The weight of the block mg acting downwards.
- The normal force N acting perpendicular to the surface of the hemisphere.
Step 2: Apply Newton's Second Law in the Radial Direction
At the point of leaving contact, the centripetal force required to keep the block moving in a circular path is provided by the component of the weight acting towards the center minus the normal force. Therefore, we can write:
mgcosθ−N=mv2R
where R is the radius of the hemisphere and v is the speed of the block at angle θ.
Step 3: Apply Conservation of Mechanical Energy
The mechanical energy of the system is conserved. Initially, when the block is at the top of the hemisphere, its potential energy is maximum and kinetic energy is zero. As it moves down, its potential energy decreases and kinetic energy increases. We can write:
Initial Potential Energy+Initial Kinetic Energy=Final Potential Energy+Final Kinetic Energy
This gives us:
mgR+0=mgRcosθ+12mv2
Rearranging this equation, we find:
mgR(1−cosθ)=12mv2
Simplifying, we get:
v2=2gR(1−cosθ)
Step 4: Substitute v2 into the Force Equation
Now, we substitute v2 from the energy conservation equation into the force equation:
mgcosθ−N=m(2gR(1−cosθ))R
This simplifies to:
mgcosθ−N=2mg(1−cosθ)
Rearranging gives:
N=mgcosθ−2mg(1−cosθ)
N=mgcosθ−2mg+2mgcosθ
N=3mgcosθ−2mg
Step 5: Set Normal Force to Zero
The block leaves the surface when the normal force N becomes zero:
3mgcosθ−2mg=0
Solving for cosθ:
3cosθ=2
cosθ=23
Step 6: Find the Angle θ
To find θ, we take the inverse cosine:
θ=cos−1(23)
Calculating this gives:
θ≈48.18∘
Final Answer
Thus, the angle θ at which the block leaves contact with the hemisphere is approximately 48.18∘.
---
When the block is at an angle θ with the vertical, two forces act on it:
- The weight of the block mg acting downwards.
- The normal force N acting perpendicular to the surface of the hemisphere.
At the point of leaving contact, the centripetal force required to keep the block moving in a circular path is provided by the component of the weight acting towards the center minus the normal force. Therefore, we can write:
mgcosθ−N=mv2R
where R is the radius of the hemisphere and v is the speed of the block at angle θ.
The mechanical energy of the system is conserved. Initially, when the block is at the top of the hemisphere, its potential energy is maximum and kinetic energy is zero. As it moves down, its potential energy decreases and kinetic energy increases. We can write:
Initial Potential Energy+Initial Kinetic Energy=Final Potential Energy+Final Kinetic Energy
This gives us:
mgR+0=mgRcosθ+12mv2
Rearranging this equation, we find:
mgR(1−cosθ)=12mv2
Simplifying, we get:
v2=2gR(1−cosθ)
Now, we substitute v2 from the energy conservation equation into the force equation:
mgcosθ−N=m(2gR(1−cosθ))R
This simplifies to:
mgcosθ−N=2mg(1−cosθ)
Rearranging gives:
N=mgcosθ−2mg(1−cosθ)
N=mgcosθ−2mg+2mgcosθ
N=3mgcosθ−2mg
The block leaves the surface when the normal force N becomes zero:
3mgcosθ−2mg=0
Solving for cosθ:
3cosθ=2
cosθ=23
To find θ, we take the inverse cosine:
θ=cos−1(23)
Calculating this gives:
θ≈48.18∘
Thus, the angle θ at which the block leaves contact with the hemisphere is approximately 48.18∘.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - NCERT FILE (NCERT Textbook Exercise)23videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - NCERT FILE (NCERT Additional Exercise)7videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Conceptual Questions20videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
WAVES
Similar Questions
A small block of mass m is placed on top of a smooth hemisphere also of mass m which is placed on a smooth horizontal surface. If the block begins to slide down due to a negligible small impulse, show that it will loose contact with the hemisphere when the radial line through vertical makes an angle θ given by the equaition cos3θ−6cosθ+4=0.
 View Solution
View SolutionA block mass 'm' is kept on the ground as shown in figure.

Draw F.B.D. of block.View Solution
Knowledge Check
- Question 1 - Select One or More
In fig. a small block is kept on m. then
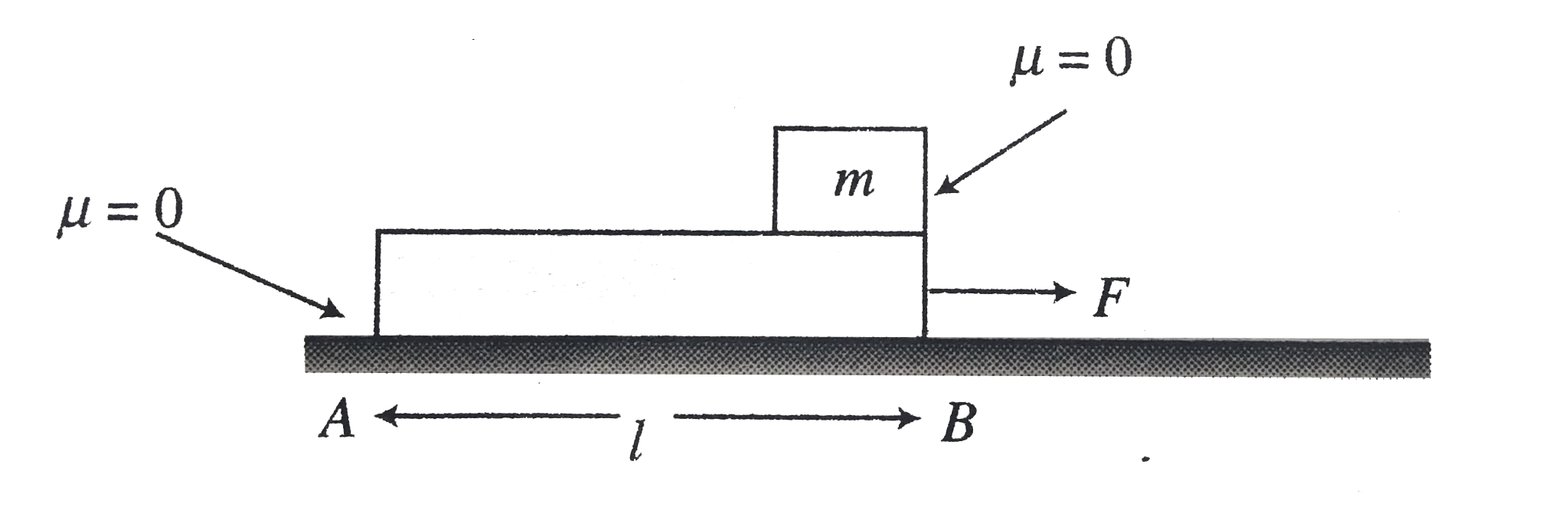 AThe acceleration of m w.r.t. ground is F/m.BThe acceleration of m w.r.t ground is zero.CThe time taken by m to separted from M is √2lmF.DThe time taken by m to separted from M is √2lMF.
AThe acceleration of m w.r.t. ground is F/m.BThe acceleration of m w.r.t ground is zero.CThe time taken by m to separted from M is √2lmF.DThe time taken by m to separted from M is √2lMF. - Question 2 - Select One
A smooth hemisphere of mass M is kept on a smooth surface. A block of mass m(=M/3) is kept on the top of the hemisphere as shown in the figure. The hemisphere is displaced slightly ang both the hemisphere and the block starts moving. At an angle θ with the vertical ( subtended by the block at the centre of the hemisphere ) , the relation between the velocity of the block ( V) and the velocity of the hemishere ( v0 ) is (V is the velocity of the block w.r.t. the hemisphere at that instant . )
 Av0=V4cosθBv0=VcosθCv0=V2sinθDv0=V2cosθ
Av0=V4cosθBv0=VcosθCv0=V2sinθDv0=V2cosθ - Question 3 - Select One
A small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?
 A32rB23rC12gt2Dv22g
A32rB23rC12gt2Dv22g
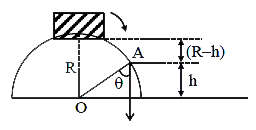
A small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m.
(Assume there is no friction between the block and the hemisphere)
 View Solution
View SolutionA small block of mass m moving on inside of the smooth hemisphere of radius R, describes a horizontal circle at a distance R/2 below the centre of the sphere. Find the time period of revolution and force with which the block pushes against the hemisphere.
View SolutionA block of mass m is placed on a smooth sphere of radius R. It slides when pushed slightly. At what vertical distance h, from the top, will it leave the sphere?
View SolutionA block of mass 70kg is kept on a rough horizontal surface (μ=0.4) . A person is trying to pull the block by applying a horizontal force, but the block is not moving. The net contact force exerted by the surface on the block is F , then:
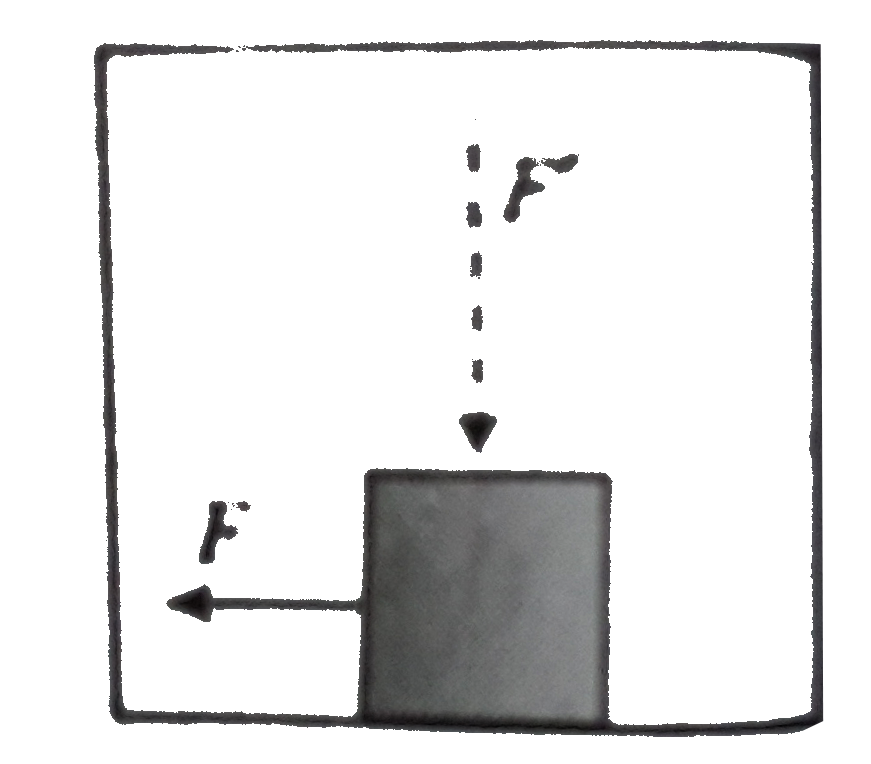
View SolutionA block of mass m is kept on the floor of a freely falling lift .During the free fall of the lift, the block is pulled horizontally with a force of F=5N,μs=0.1The friction force on the block will be
 View Solution
View Solution

