Pendulum bob of mass m connected to a string of length l is made to whirl around in a vertical circle . Maximum speed of bob is found to be double of the minimum speed . Calculate tension in the thread when velocity of the bob is directed vertically downward .
Refer to the figure remains horizontal when velocity of the bob is vertically downward .
Let v be the velocity at the highest point and so 2v is the velocity at the bottom point . We can apply coservation of mechnical energy between these two points .
Loss in K.E = gain in gravitational potential energy
12m(2v)2−12mv2=mg(2l)
⇒ 32mv2=mg(2l)
⇒ v=√4gl3 ...(i)
We can now apply conservation of mechanical energy between highest point and the point where string is horizontal.
Gain in K.E = loss in gravitational potential energy
12mu2−12mv2=mgl
Substituting from equation (i) we get
12mu2−2mgl3=mgl
⇒ 12mu2=53mgl
⇒ mu2l=103mg ...(ii)
Applying circular dynamics at point where string is horizontal we get
T=mu2l
Using equation (ii) we can write
T=103 mg

Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - NCERT FILE (NCERT Textbook Exercise)23videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - NCERT FILE (NCERT Additional Exercise)7videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Conceptual Questions20videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
WAVES
Similar Questions
A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure. What will be X the trajectory of the particle if the string is cut at
(a) Point B
(b) Point C
(c) Point X
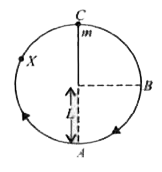 View Solution
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at
(a) Point B ? (b) Point C? (c) Point X?
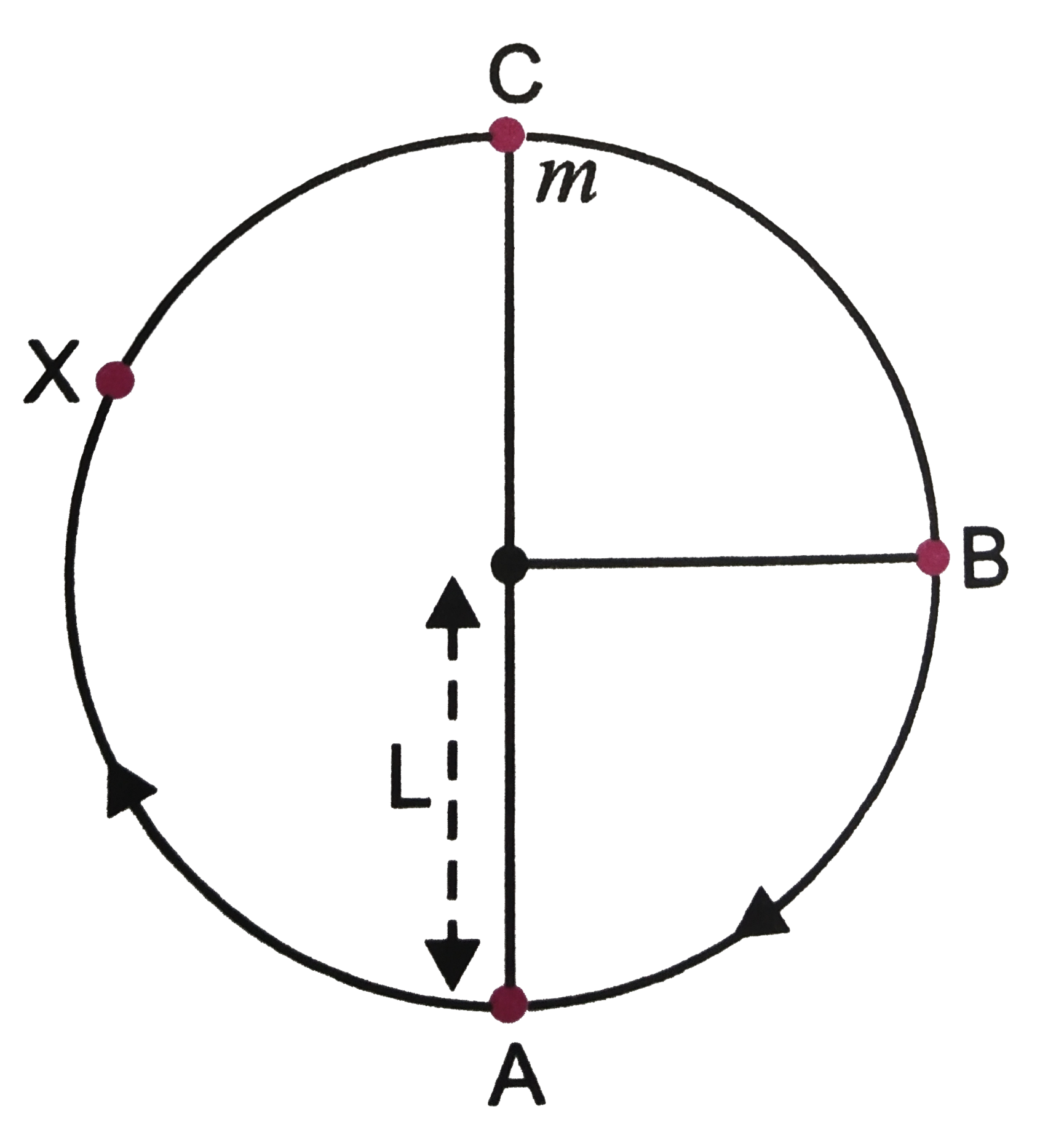 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is whirled in a vertical circle with the help of a thread. If− the maximum tension in the thread is double its minimum value then the value of minimum tension in the thread will be:
A6 mgBzeroC3 mgDcan't be found - Question 2 - Select One
A simple pendulum of bob of mass m and length L has one of its ends fixed at the centre O of a vertical circle, as shown in the figure. If 0=60∘ at the point P, the minimum speed u that should be given to the bob so that it completes vetical circle is
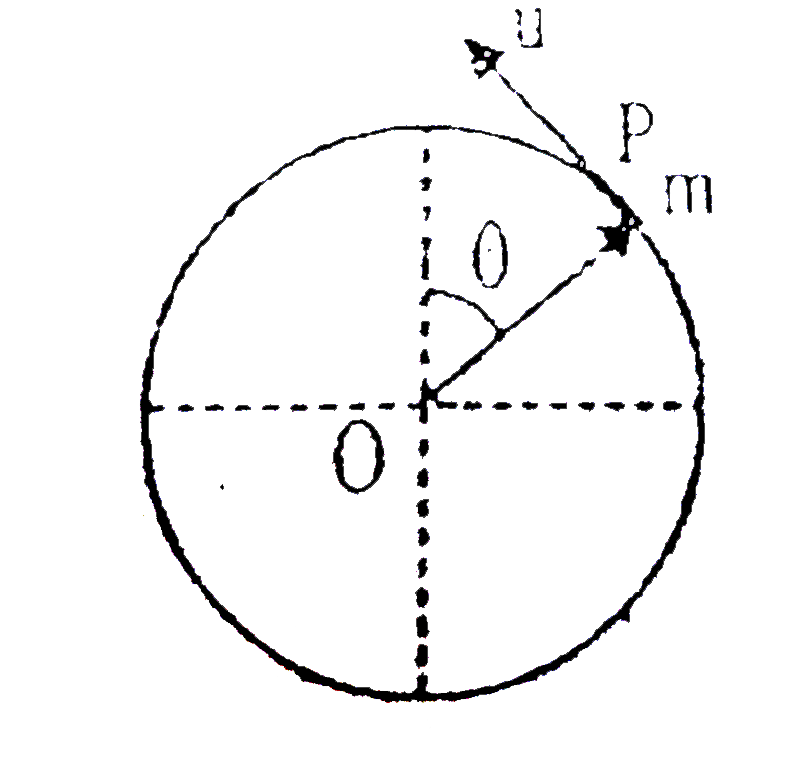 A√gLB√2gLC√5gL2D√3gL2
A√gLB√2gLC√5gL2D√3gL2 - Question 3 - Select One
A pendulum bob is rotated in a vertical circle with one end of string of length l fixed at a position . At a certain instant bob is at its lowest position and is moving with speed u . Calculate the magnitude of change in velocity when string becomes horizontal for a moment .
A√(u2−gl)B√2(u2−gl)C√3(u2−gl)D2√(u2−gl)
A simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionConsider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.
 View Solution
View SolutionA small bob tied at one end of a thin string of length 1m is describing a vertical circle so that the maximum and minimum tension in the string are in the ratio 5: 1. The velocity of the bob at the height position is ____ m/s. (Take g=10m/s2)
View SolutionBob of the simple pendulum is at rest at its lowest position , Sharp hit imparts a speed of √9gl to the pendium bob. Calculate tension of the thread when it makes an angle 60∘ with the vertical .
View SolutionA simple pendulum bob of mass M and length l has one of its end fixed at the centre of a vertical circle as shown in figure. If θ=60∘ at the point P, the minimum speed u that should be given to the bob so that it completes vertical circle is :
 View Solution
View Solution

