CD and GH are respectively the bisectors of and such that D and H lie on sides AB and FE of respectively. IF then show that
Step by step video solution for CD and GH are respectively the bisectors of angle ACB and angle EGF such that D and H lie on sides AB and FE of DeltaABC and Delta FEG respectively. IF DeltaABC~DeltaFEG then show that (CD)/(GH)=(AC)/(FG) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- సరూప త్రిభుజాలుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - సరూప త్రిభుజాలుEXERCISE - Exercise
211 Videos
- సమితులుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - సమితులుEXERCISE - Exercise
298 Videos
- సాంఖ్యకశాస్తంBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - సాంఖ్యకశాస్తంEXERCISE - Exercise
147 Videos
Similar Questions
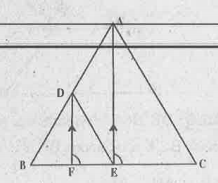
ఇచ్చిన పటంలో, DE∣∣AC మరియు DF∣∣AE అయిన BF /FE = BE/ EC అని చూపండి.
View Solutionక్రింది వాటిలో ఏవి సమితులు? మీ సమాధానాన్ని సహేతుకంగా సమర్థించండి. "J" అనే అక్షరంతో ప్రారంభమయ్యే ఒక సంవత్సరంలో గల అన్నీ నెలల సమూహాలు.
View Solutionఒక' గ్రామంలో కొంతమంది విద్యార్థుల జట్టు “పర్యావరణ పరిరక్షణ - అవగాహని అనే కార్యక్రమంలో భాగంగా, 20 ఇండ్లలో సర్వే నిర్వహించి, ఎన్నెన్ని మొక్కలు నాటినారో సమాచారాన్ని సేకరించి, ఈ క్రింది పట్టికలో నమోదు చేసినారు. సగటున ఒక ఇంటికి ఎన్ని మొక్కలు నాటినారో కనుక్కోండి.

View SolutionIn the given figure, CD and GH are respectively the bisectors of angle ACB and angle FGE "of" Delta ABC and Delta EFG respectively . If Delta ABC~ Delta FEG , prove that : (a) Delta ADC~ Delta FHG " " (b) Delta BCD ~ Delta EGH " " ( c ) (CD)/(GH)=(AC)/(FG)
View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionCD and GH are the bisectors of ∠ACB and ∠EGF respectively. If D lies on AB of ΔABC and H lies on EF of ΔEFG and if ΔABC~ΔEFG, then prove that (a) CDGH=ACFG, (b)ΔDCB~ΔHGE, (c)ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
CDGH=ACFG
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCB~ΔHGE
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCA~ΔHGF
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
CDGH=ACFG
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCB~ΔHGE
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCA~De<HGF
View SolutionCD and GH are respectively the bisectors of ⌊ACBand⌊EGF such that D and H lie on sidea AB and FE of ΔABCandΔEFG respectively. If ΔABC~ΔFEG, show that.
i] CDGH=ACFG
ii] ΔCDB~ΔHGE
iii] ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
CDGH=ACFG
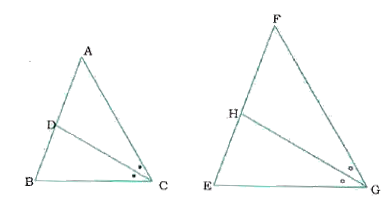
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
ΔDCB~ΔGHE
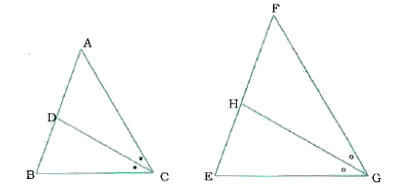
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
ΔDCA~ΔHGF

View Solution
