→OA and →BO are two vectors of magnitudes 5 and 6 respectively.If ∠(BOA)=60∘, then −−→OA.−−→OB is equal toSolution in Kannada
0
15
−15
15√3
The correct Answer is:B
Step by step video, text & image solution for vec OA and vec BO are two vectors of magnitudes 5 and 6 respectively.If angle (BOA) = 60^(@), then vec (OA) .vec(OB) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If p→(q∨r) is false, then the truth values of p,q,r are respectively
View SolutionOn the set Z , of all integers ∗ is defined by a∗b=a+b−5. If 2∗(x∗3)=5 then x=
View SolutionIf the projection of Vector vec OA on unit vector vec OB equals twice the area of Delta OAB in magnitude,then /_AOB is
View SolutionThe magnitudes of vectors vec OA,vec OB and vec OC( in figure( 2-W3) are equal.Find the direction of )/(Ovec A)+vec OB-vec OC.
View SolutionFind the resultant of the three vectors vec OA,vec OB and vec OC each of magnitude r as shown in figure?
View SolutionIf −−→OA=2ˆi+3ˆj−4ˆkand−−→OB=ˆj+ˆk are two vectors through the origin O, find the projection of −−→OAand−−→OB
View SolutionIf −−→OA=2ˆi+3ˆj−4ˆkand−−→OB=ˆj+ˆk are two vectors through the origin O, find the projection of −−→OBon−−→OA.
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionThe resultant of vectors −−→OAand−−→OB is peerpendicular to vec(OA). Find the angle AOB.
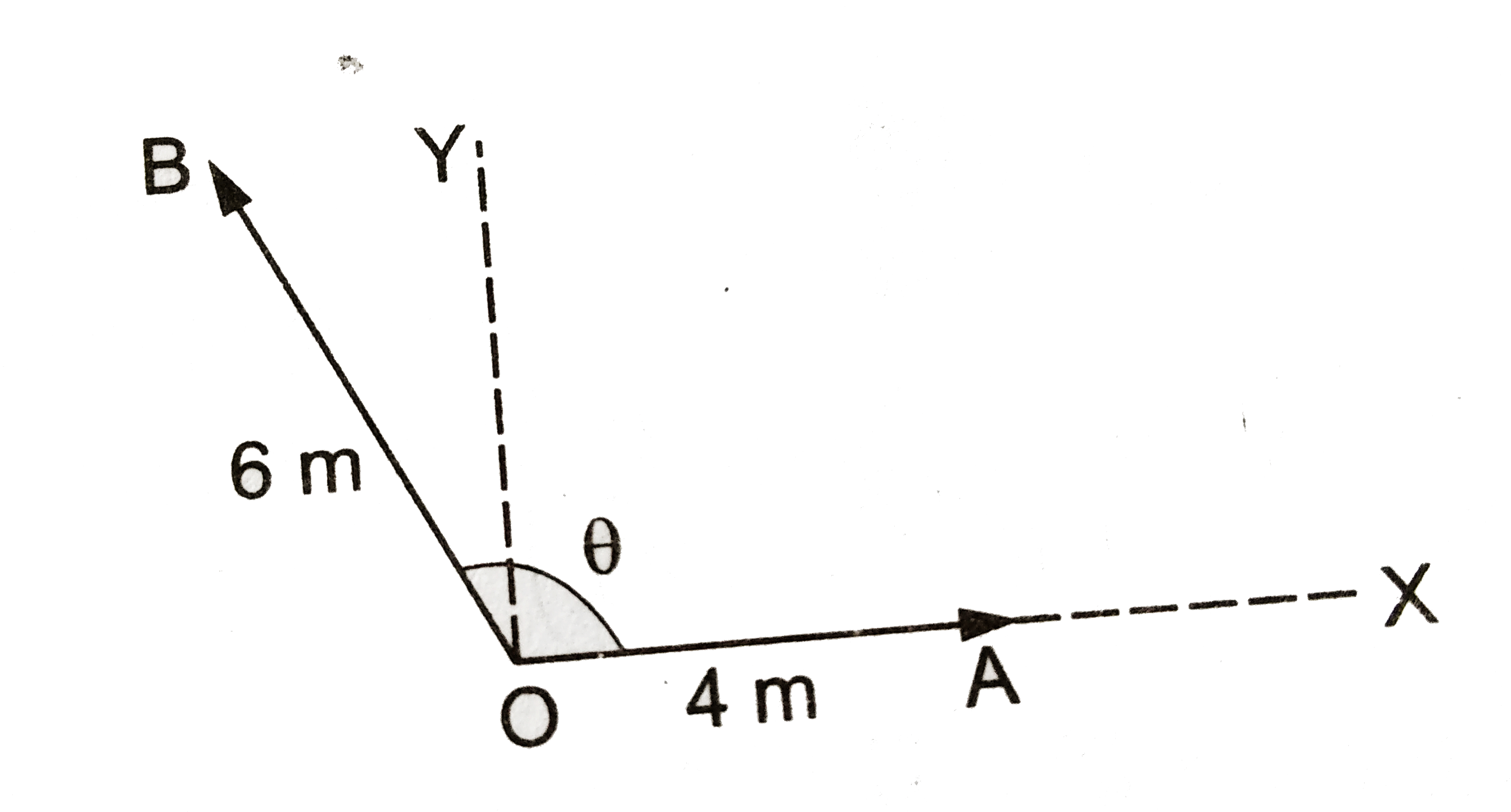
View Solutionदिखाए गए वेक्टरो −−→OA,−−→OB तथा −−→OC के परिमाण बराबर है। वेक्टर −−→OA+−−→OB−−−→OC की दिशा बताएँ।
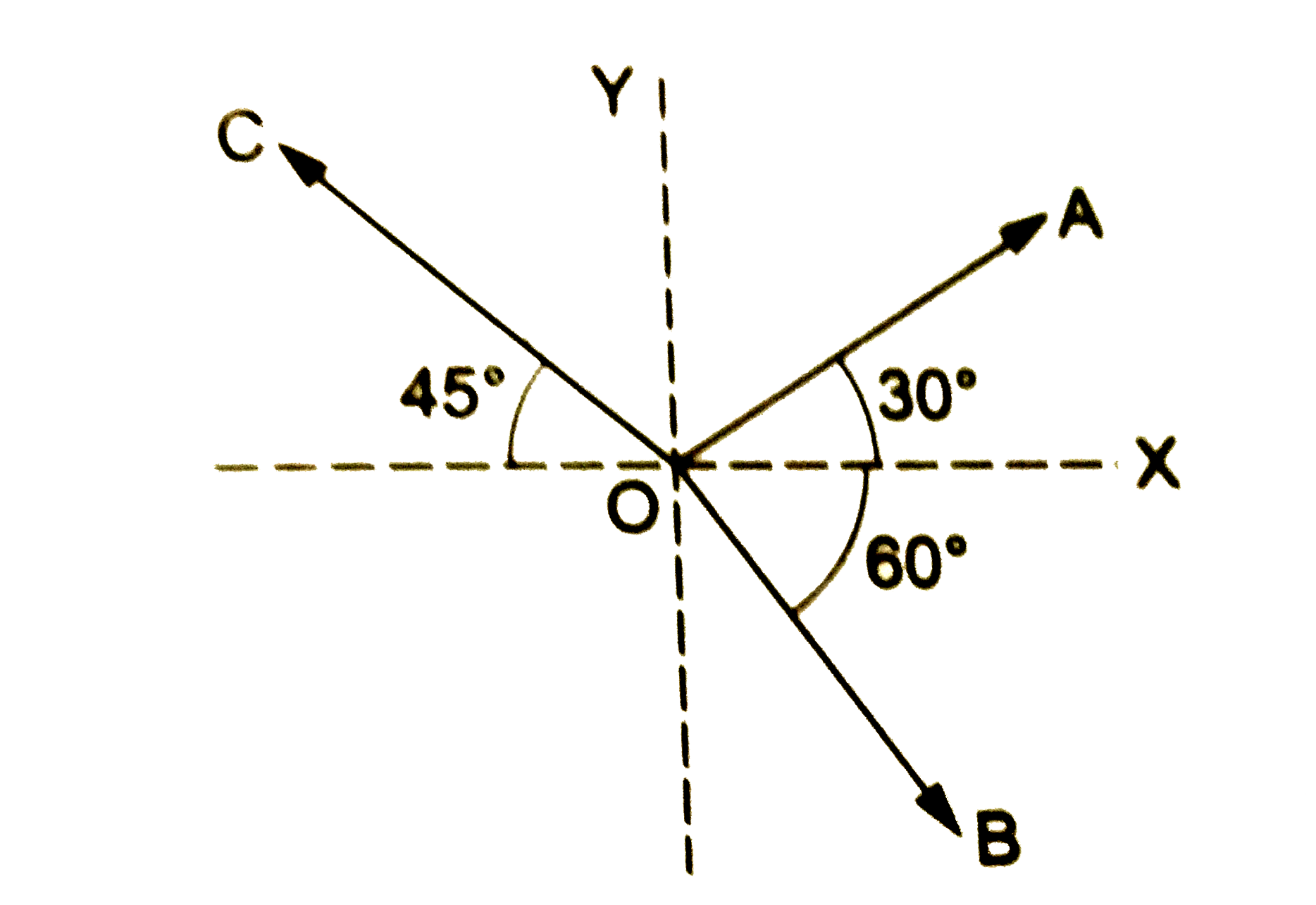
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionThe resultant of vectors −−→OAand−−→OB is perpendicular to −−→OA. Find the angle AOB.

View Solution−−→OAand−−→BO are two vectors of magnitudes 5 and 6 respectively. If ∠BOA=60∘,then −−→OA.−−→OB is equal to
View Solution
