Let S(α)={(x,y):y2≤x,0≤x≤α}andA(α) is area of the regions S(α). If for λ,0<λ<4,A(λ):A(4)=2:5, then λ equals
A
2(425)13
B
4(25)13
C
4(425)13
D
2(25)13
Text Solution
The correct Answer is:C
Given, S(α)={(x,y):y2≤x,0≤x≤α}andA(α) is area of the region S(α)
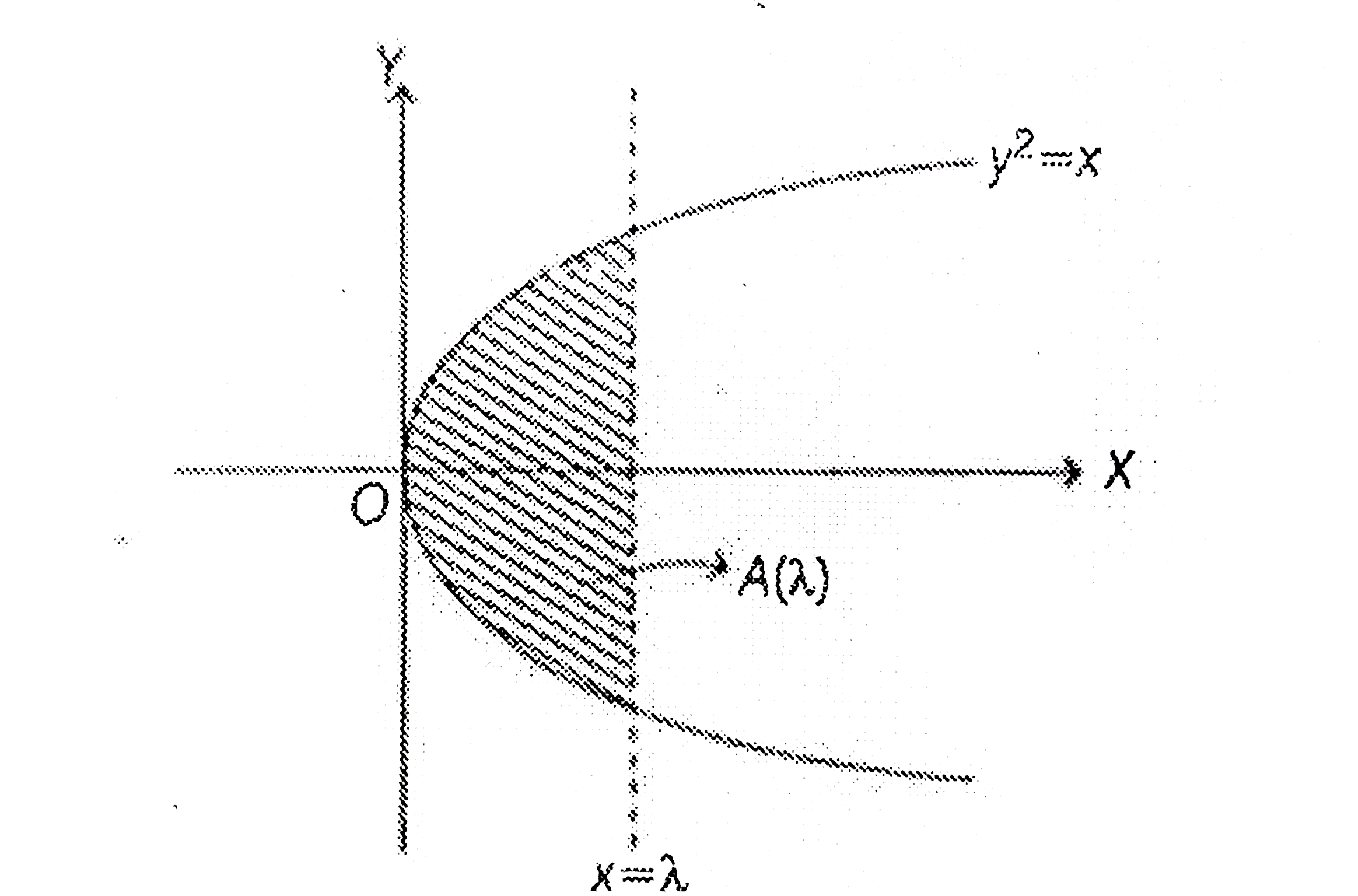
Clearly, A(λ)=2∫λ0√xdx=2[x3/23/2]λ0=43λ3/2
Since, A(λ)A(4)=25,(0<λ<4)
⇒λ3/243/2=25⇒(λ4)3=(25)2
⇒λ4=(425)1/3⇒λ=4(425)1/3
|
Topper's Solved these Questions
- AREABOOK - IIT JEE PREVIOUS YEARCHAPTER - AREAEXERCISE - AREA USING INTEGRATION
55 Videos
- APPLICATION OF DERIVATIVES BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)
8 Videos
- BINOMIAL THEOREMBOOK - IIT JEE PREVIOUS YEARCHAPTER - BINOMIAL THEOREMEXERCISE - Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
8 Videos
Similar Questions
Knowledge Check
If 0≤α≤2π and ∫α0cosxdx=cos2α, the : α=
Aπ6Bπ3Cπ2Dπ4Let f(x,y)={(x,y):y2≤4x,0≤x≤λ} and s(λ) is area such that S(λ)S(4)=25. Find the value of λ.
A4(424)1/3B4(225)1/3C2(425)1/3D2(225)1/3If the area (in sq. units) bounded by the parabola y2=4λx and the line y=λx,λ>0, is 19, then λ is equal to:
A2√6B48C24D4√3
If α,β are the roots of x2–3x+λ=0(λ∈R) and α<1<β, then the true set of values of λ equals
View SolutionIf α and β are the roots of the equation x2+6x+λ=0 and 3α+2β=−20 ,then λ=
View SolutionIf α and β are the roots of the equation x2−5λx−λ2=0 and α2+β2=274 ,then the value of λ2 is
View SolutionIf (x+y)2=2(x2+y2) and (x–y+λ)2=4,λ>0, then λ is equal to
View SolutionSolve : tan2α+secα−1=0,0≤α<2π.
View Solution
