Find the area bounded by the curve $x^{2} = 4 y$ and the straight line $x = 4 y - 2 .$

A

$\frac{7}{8}$

B

$\frac{9}{8}$

C

$\frac{5}{4}$

D

$\frac{3}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Given equation of curve is $x^{2} = 4 y,$ which represent a parabola with vertex (0, 0) and it open upward.

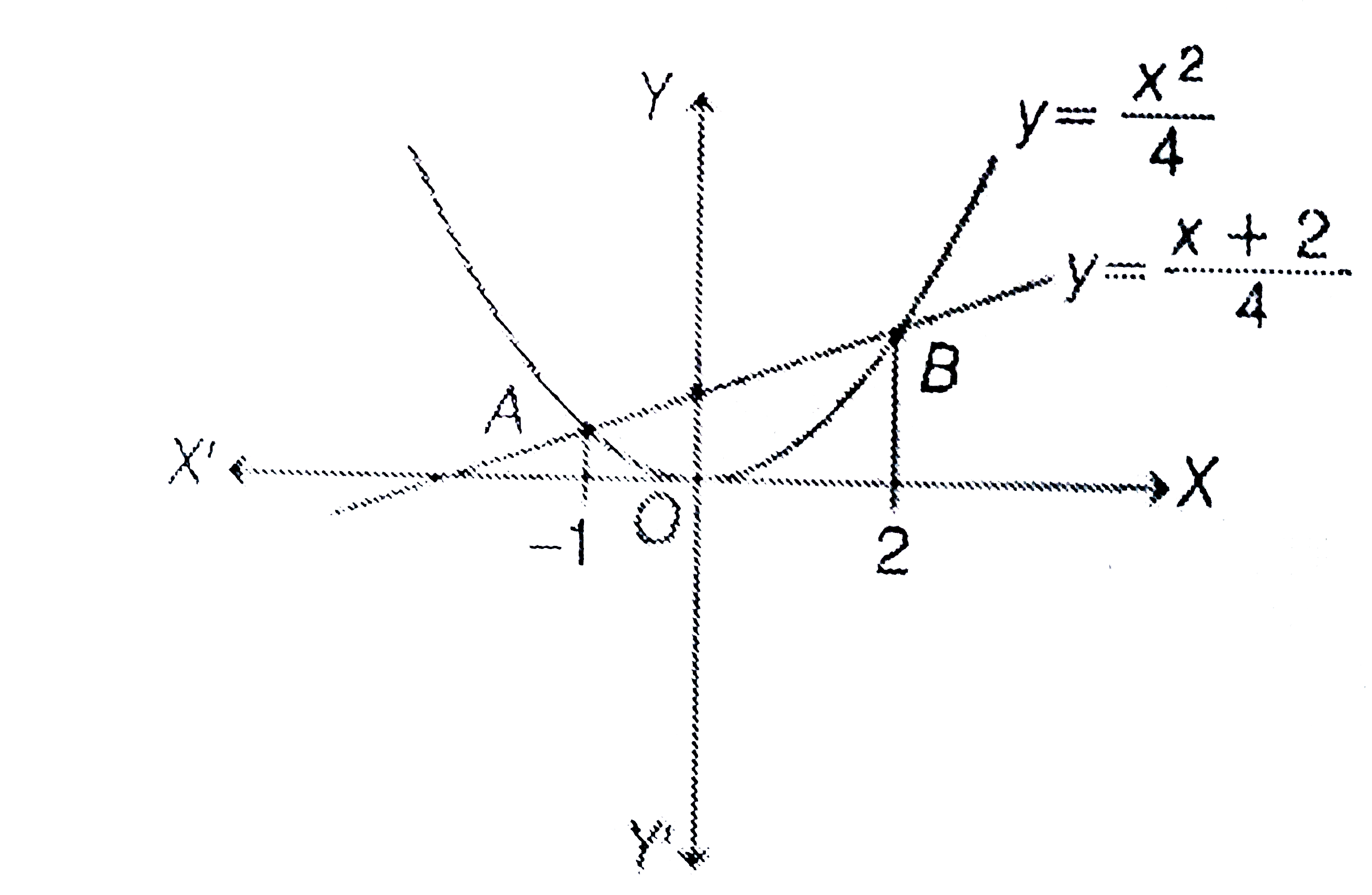
Now, let us find the points of intersection of $x^{2} = 4 y$ and $4 y = x + 2$ .
For this consider, $x^{2} = x + 2$
$\Rightarrow x^{2} - x - 2 = 0$
$\Rightarrow (x - 2) (x + 1) = 0$
$\Rightarrow x = - 1, then y = \frac{1}{4}$
and when $x = 2, then y = 1$
Thus, the points of intersection are $A (- 1, \frac{1}{4}) and B (2, 1) .$
Now, required area = area of shaded region
$= \int_{- 1}^{2} {y (line) - y (parabola)} d x$
$= \int_{- 1}^{2} (\frac{x + 2}{4} - \frac{x^{2}}{4}) d x = \frac{1}{4} {[\frac{x^{2}}{2} + 2 x - \frac{x^{3}}{3}]}_{- 1}^{2}$
$= \frac{1}{4} [(2 + 4 - \frac{8}{3}) - (\frac{1}{2} - 2 + \frac{1}{3})]$
$= \frac{1}{4} [8 - \frac{1}{2} - 3] = \frac{1}{4} [5 - \frac{1}{2}] = \frac{9}{8}$ sq units.

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area of the region bounded by the curve $x^{2} = 4 y$ and the straight line $x = 4 y - 2$ is
A $\frac{3}{8} sq units$
B $\frac{5}{8} sq unit$
C $\frac{7}{8} sq unit$
D $\frac{9}{8} sq units$
The area of the region bounded by the curve $x^{2} = 4 y$ and the straight line $x = 4 y - 2$ is
A $\frac{3}{8} sq units$
B $\frac{5}{8} sq unit$
C $\frac{7}{8} sq unit$
D $\frac{9}{8} sq units$

IIT JEE PREVIOUS YEAR-AREA-AREA USING INTEGRATION

Home
Ask Doubt
Profile