The spool shown in figure is placed on a rough surface has inner radius r and outer radius R. The angle θ between the applied force and the horizontal can be varied. The critical angle (θ) for which the spool does not roll and remains stationary is given by

sinθ=rR
cosθ=rR
cosθ=√rR
cosθ=2rR
The correct Answer is:B
For spool to be stationary, ΣF=0
or Fcosθ−f=0 ...(i)
Also, Στ=0,
or Fr−fR=0 ...(ii)
From above equation,
cosθ=rR

Topper's Solved these Questions
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-1 : CONCEPT BUILDER
58 Videos
- SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - DISHA PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - EXERCISE -2: CONCEPT APPLICATOR
25 Videos
- THERMAL PROPERTIES OF MATTER BOOK - DISHA PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - Exercise-2 (Concept Applicator)
28 Videos
Similar Questions
The spool shown in the figure is placed on a rough horizontal surface and has inner radius r and outer radius R. The angle θ between the applied force and the horizontal can be varied. The critical angle θ for which the spool does not roll and remains stationary is given by

View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

View Solution
Knowledge Check
The spool shown in the figure is placed on a rough horizontal surface and has inner radius r and outer radius R. The angle θ between the applied force and the horizontal can be varied. The critical angle θ for which the spool does not roll and remains stationary is given by
 Aθ=cos−1(rR)Bθ=cos−1(2rR)Cθcos−1√rRDθ=sin−1(rR)
Aθ=cos−1(rR)Bθ=cos−1(2rR)Cθcos−1√rRDθ=sin−1(rR)A hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
 Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.
Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.A time varying force is applied on a block placed over a rough surface as shown in figure. Let θ be the angle between net contact force on the block and the normal reaction, then with time, θ will
 Aremain constantBfirst increase to a maximum value (say θmax) and then becomes constant in a value less then θmaxCfirst decrease to a minimum value (say θmin) and then becomes constant in a value more then θminDNone of the above
Aremain constantBfirst increase to a maximum value (say θmax) and then becomes constant in a value less then θmaxCfirst decrease to a minimum value (say θmin) and then becomes constant in a value more then θminDNone of the above
A spool has the shape shown in figure. Radii of inner and outer cylinders are R and 2 R respectively. Mass of the spool is 3m and its moment of inertia about the shown axis is 2mR2. Light threads are tightly wrapped on both the cylindrical parts. The spool is placed on a rough surface with two masses m1=m and m2=2m connected to the strings as shown. The string segment between spool and the pulleys P1 and P2 are horizontal. The centre of mass of the spool is at its geometrical centre. System is released from rest.
(a) What is minimum value of coefficient of friction between the spool and the table so that it does not slip?
(b) Find the speed of m1 when the spool completes one rotation about its centre.

View Solution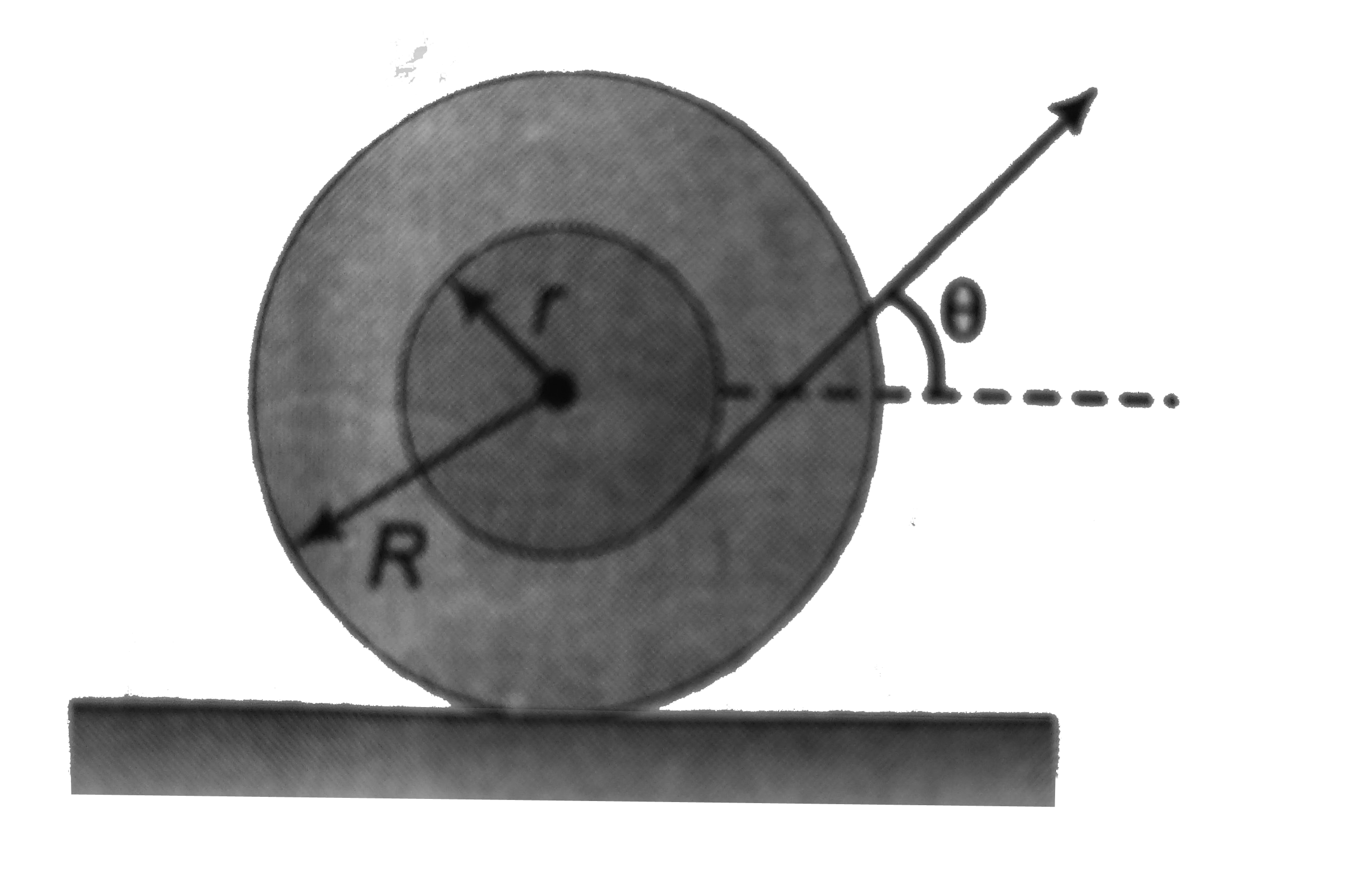
A spool is pulled at an angle θ with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle θ is equal to
View SolutionA hollow cylinder of specific resistance ρ, inner radius R, outer radius 2R and length 1 is as shown in figure. What is the net resistance between the inner and outer surfaces?
View SolutionA hollow cylinder of specific resistance ρ, inner radius R, outer radius 2R and length l is as shown in figure. What is the net resistance between the inner and outer surfaces?
View Solution
A spool is pulled at an angle θ with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle θ is equal to
View Solution
