A tennis ball (treated as hollow spherical shell) starting from O rolls down a hill. At point A the ball becomes air borne leaving at an angle of with the horizontal. The ball strickes the ground at B. What is the value of the distance AB?
(Moment of inertia of a spherical shell of mass m and radius R about its diameter = )

The correct Answer is:B
Velocity of the tennis ball on the surface of the earth or ground
(where k = radius of gyration of spherical shell = )
Horizontal range AB
Topper's Solved these Questions
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-1 : CONCEPT BUILDER
58 Videos
- SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - DISHA PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - EXERCISE -2: CONCEPT APPLICATOR
25 Videos
- THERMAL PROPERTIES OF MATTER BOOK - DISHA PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - Exercise-2 (Concept Applicator)
28 Videos
Similar Questions
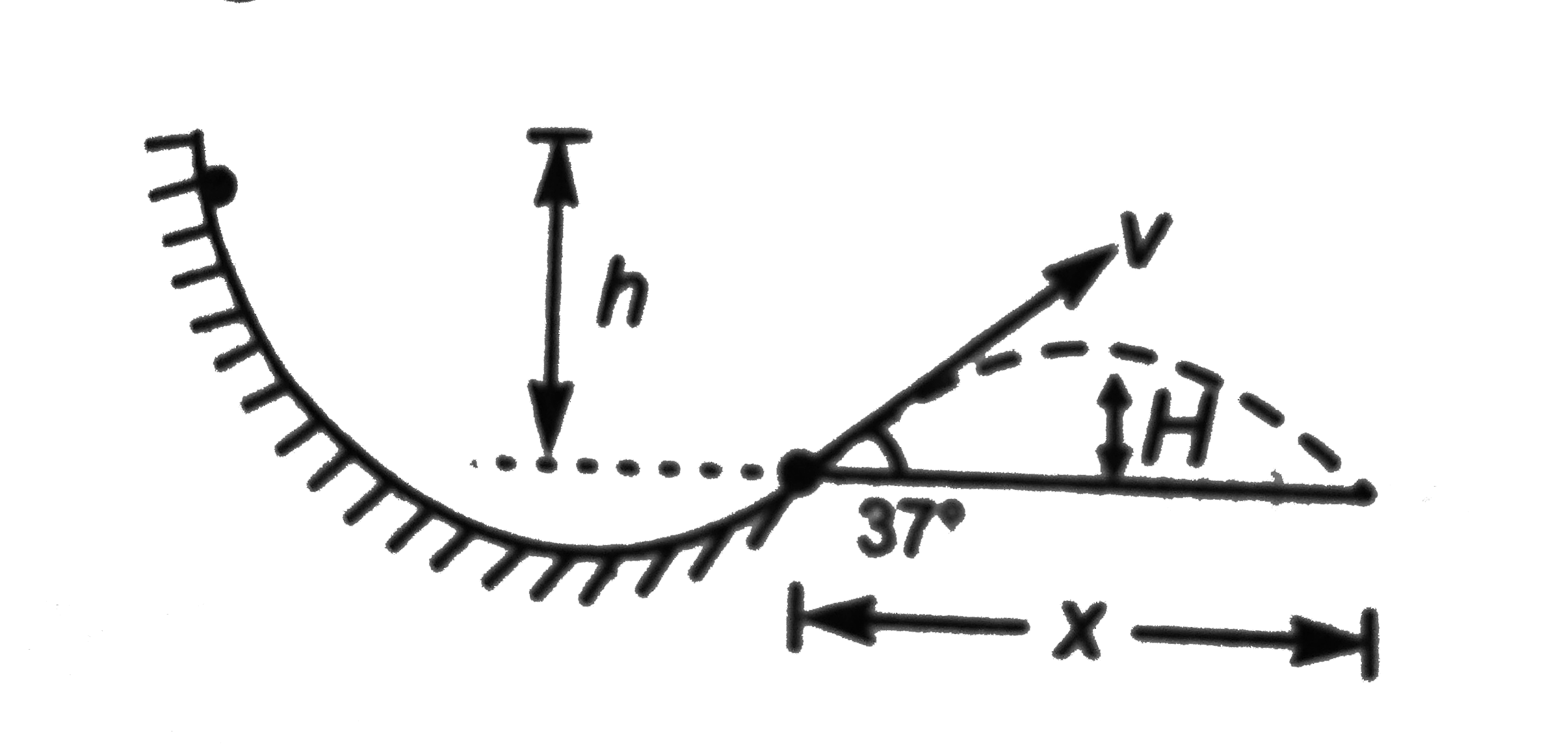
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Range x of the ball is
View Solution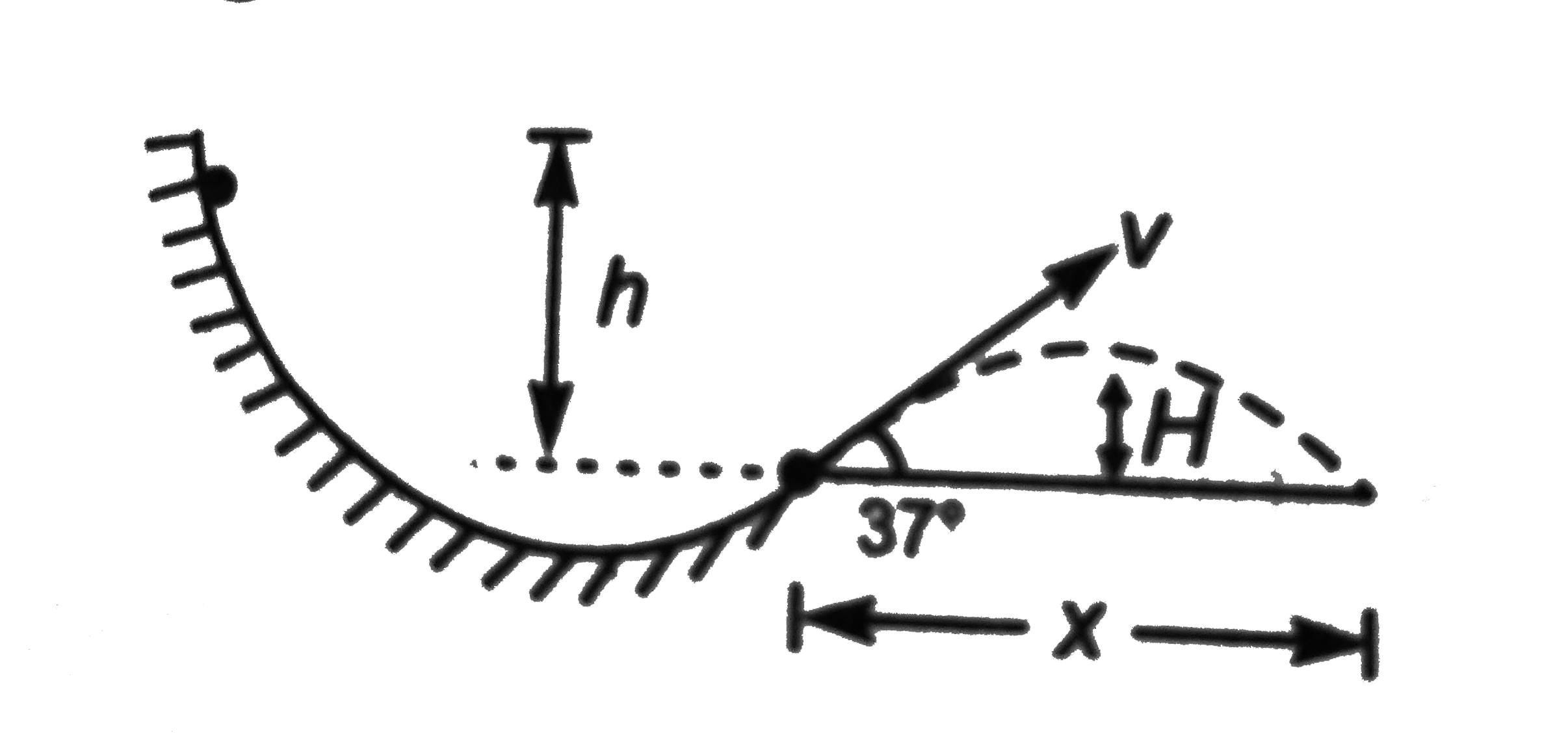
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Maximum height reached by ball H above ground is
View Solution
Knowledge Check

A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Range x of the ball isA144125hB4825hC4835hD247h
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Maximum height reached by ball H above ground isA9h35B18h35C18h25D27h125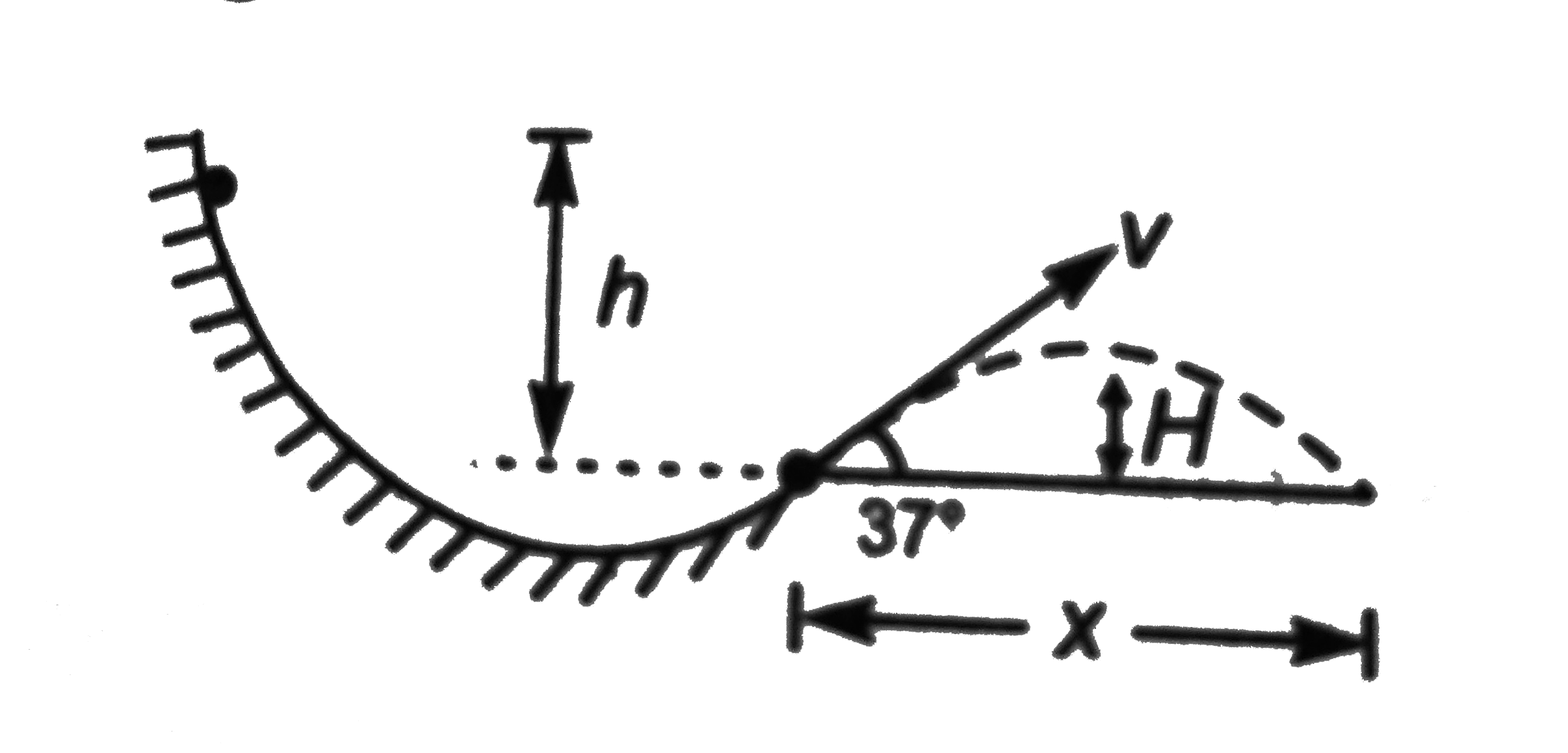
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. The velocity of projection v isA√2ghB√107ghC√57ghD√65gh

A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. The velocity of projection v is
View Solution(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5,whereM is the mass of the sphere and R is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be 14MR2, find the moment of inertia about an axis normal to the disc passing through a point on its edge.
View SolutionA ball is thrown from a point O aiming a target at angle 30∘ with the horizontal so that the ball hits the target at B but the ball hits at point A, a vertical distance h below B. If the intial velocity of the ball is 20ms−1 and the horizontal distance between O and C is 10 m. Find the value of h.

View SolutionThe moment of inertia of thin spherical shell of mass M and radius R about a diameter is 23MR. Its radius of gyration K about a tangent will be
View SolutionA ball is thrown from a point O aiming a target at angle 30∘ with the horizontal so that the ball hits the target at B but the ball hits at point A, a vertical distance h below B. If the intial velocity of the ball is 20ms−1 and the horizontal distance between O and C is 10 m. Find the value of h.

View Solution
