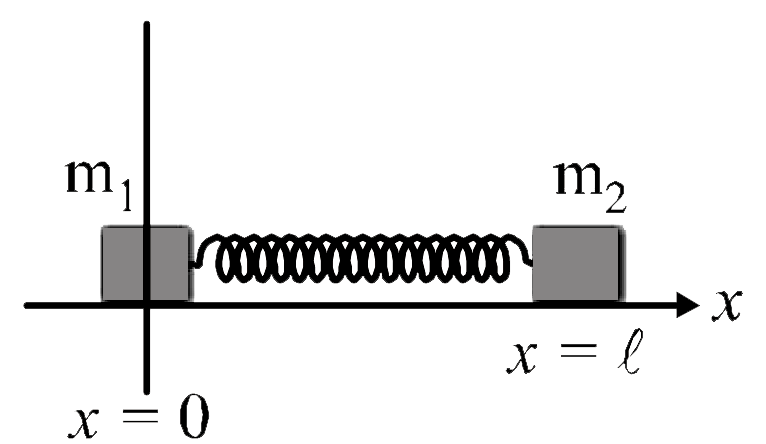
Two masses $m_{1} and m_{2}$ are connected by a massless spring of spring constant k and unstretched length l. The masses are placed on a frictionless straight channel, which are consider our x-axis. They are initially at $x = 0 and x = l$ respectively. At t = 0, a velocity $v_{0}$ is suddenly imparted to the first particle. At a later time t, the centre of mass of the two masses is at :

A

$x = \frac{m_{2} l}{m_{1} + m_{2}}$

B

$x = \frac{m_{1} l}{m_{1} + m_{2}} + \frac{m_{2} v_{0} t}{m_{1} + m_{2}}$

C

$x = \frac{m_{2} l}{m_{1} + m_{1}} + \frac{m_{2}_v_{0} t}{m_{1} + m_{2}}$

D

$x = \frac{m_{2} l}{m_{1} + m_{2}} + \frac{m_{1} v_{0} t}{m_{1} + m_{2}}$

Text Solution

Verified by Experts

The correct Answer is:D

Initial position of $c m = \frac{m_{2} l}{m_{1} + m_{2}}$
Also $x_{c m} = \frac{m_{1} Δ x_{1} + m_{2} Δ x_{2}}{m_{1} + m_{2}} = \frac{m_{1} v_{0} t + 0}{m_{1} + m_{2}}$
$∴$ final position = $\frac{m_{2} l}{m_{1} + m_{2}} + \frac{m_{1} v_{0} t}{m_{1} + m_{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS SYSTEM OF PARTICLES & ROTATIONAL MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two masses $m_{1}$ and $m_{2}$ are connected by a massless spring of spring constant k and unstreched length l. The masses are placed on a frictionless straight channel – which we consider our x-axis. They are initially at rest at x = 0 and x = l, respectively. At t = 0, a velocity of v0 is suddenly imparted to the first particle. At a later time t0, the centre of mass of the two masses is at-
A $x = \frac{m_{2} l}{m_{1} + m_{2}}$
B $x = \frac{m_{1} l}{m_{1} + m_{2}} + \frac{m_{2} v_{0} t}{m_{1} + m_{2}}$
C $x = \frac{m_{2} l}{m_{1} + m_{2}} + \frac{m_{2} v_{0} t}{m_{1} + m_{2}}$
D $x = \frac{m_{2} l}{m_{1} + m_{2}} + \frac{m_{1} v_{0} t}{m_{1} + m_{2}}$
Question 2 - Select One
Two masses $m_{1}$ and $m_{2}$ connected by a spring of spring constant k rest on a frictionless surface. If the masses are pulled apart and let go, the time period of oscillation is-
A $T = 2 π \sqrt{\frac{1}{k} (\frac{m_{1} m_{2}}{m_{1} + m_{2}})}$
B $T = 2 π \sqrt{\frac{1}{k} (\frac{m_{1} + m_{2}}{m_{1} m_{2}})}$
C $T = 2 π \sqrt{(\frac{m_{1}}{k})}$
D $T = 2 π \sqrt{(\frac{m_{2}}{k})}$
Question 3 - Select One
Two blocks of masses $m_{1}$ and $m_{2}$ are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separately
Bthe magnitude of momentums of each body are equal to each other
Cthe mechanical energy of system remains constant
Dboth (C) and (B) are correct

DISHA PUBLICATION-SYSTEM OF PARTICLES & ROTATIONAL MOTION -EXERCISE-2 : CONCEPT APPLICATOR

Home
Ask Doubt
Profile