Two parallel glass plates are dipped partly in the liquid of density d keeping them vertical. If the distance between the plates is x surface tension for the liquid is T and angle of contact θ, then rise of liquid between the plates due to capillary will be
Tcosθxd
2Tcosθxeg
2Txdgcosθ
Tcosθxdg
The correct Answer is:B
Let the width of each plate is b and due to surface tension liquid will rise upto height h then upward force due to surface tension
=2Tbcosθ …(i)
Weight of the liquid rises
in between the plates
=Vdg=(bxh)dg ...(ii)

Equation (i) and (ii) we get, 2Tcosθ=xhdg
∴h=2Tcosθxdg
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - DISHA PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-1 CONCEPT BUILDER
59 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
- MOTION IN A PLANE BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -2 : CONCEPT APPLICATOR
28 Videos
Similar Questions
The distance between the plates fo a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates, what will be the new capacity ?
View Solution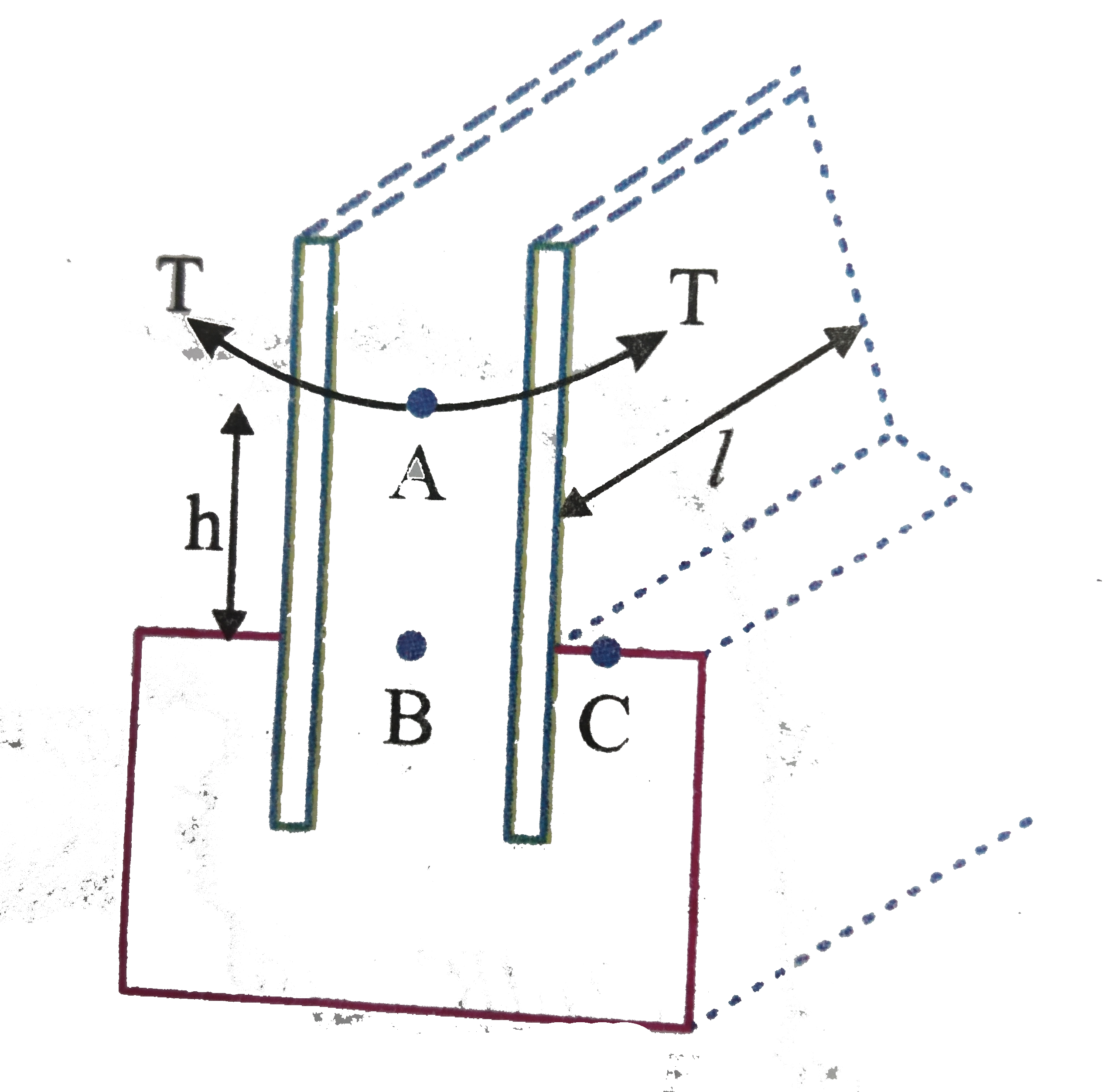
Expression for the height of capillary rise between two parallel plates dipping liquid of density σ separated by a distance d. The surface tension of the liquid is T. [Take angle of contact to be zero]
View Solution
Knowledge Check
Two parallel glass plates are dipped partly in the liquid of denstiy 'd' keeping them vertical. If the distance between the plates is 'x', Surface tension is T and angle of contact is θ then ries of liquid between the plates due to capillary will be
ATcosθxdB2TcosθxdgC2TxdgcosθDtcosθxdgTwo parallel glass plates separated by a small distance x ar dipped partly in a liquid of density ' d keeping them vertical .The surface tension of the liquid is T and angle of contact is θ . What is the rise of the liquid between the plates due to capillarity ?
A2TcosθxdgB2TxdgcosθCTcosθxdgDTcosθxdTwo vertical glass plates 1 mm apart are dipped into water. How high will the water rise between the plates. If the surface tension of water is 70 dyne cm−1
A1.43 cmB1.63 cmC2.86 cmD3.86 cm
The distance between the plates fo a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates, what will be the new capacity ?
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View SolutionIn a parallel plate capacitor, the distance between the plates is d and potential difference across the plate is V. Energy stored per unit volume between the plates of capacitor is
View SolutionTwo parallel glass plates are held vertically at a small separation d and dipped in a liquid of surface tension T , the angle of contact θ=0∘ and density ρ . The height of water that climbs up in the gap between glass plates is given by
View SolutionTwo vertical parallel glass plates are partially submerged in water. The distance between the plates is d and the length is l. Assume that the water between the plates does not reach the upper edges of the plates and the wetting is complete. The water will rise to height (ρ= density of water and α= surface tension of water)
View Solution
