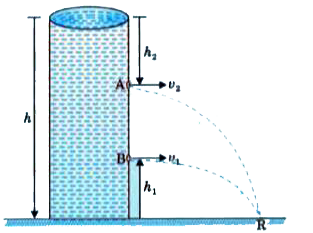
I a cylindrical water tank, there are two small holes A and B on the wall at a depth of h1, from the surface of water and at a height of h2 from the bottomof water tank. Surface of water is at height of h2 from the bottom of water tank. Surface of water is at height H from the bottom of water tank. Water coming out from both holes strikes the ground at the same point S. FInd the ratio of h1andh2

Depends on H
1:1
2:2
1:2
The correct Answer is:A
Range is same for both holes
∴2√(H−h1)h1=2√(H−h2)h2
Squaring both sides,
4(H−gh1)h1=4(H−h2)h2
Hh1−h21=Hh2−h22
On solving we get, H=h1+h2
Hence, the ratio of h1h2 depends on H.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - DISHA PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-1 CONCEPT BUILDER
59 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
- MOTION IN A PLANE BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -2 : CONCEPT APPLICATOR
28 Videos
Similar Questions
In a cylindrical water tank there are two small holes Q and P on the wall at a depth of h1 from the upper level of water and at a height of h2 from the lower end of the tank, respectively, as shown in the figure. Water coming out from both the holes strike the ground at the same point. The ratio of h1 and h2 is

View SolutionOn the wall of a cylindrical water tank, two holes are made as shown in figure. Water coming out from these holes hits the ground at the same point. What will be the ration h1h2?
View Solution
Knowledge Check
In a cylindrical water tank there are two small holes Q and P on the wall at a depth of h1 from the upper level of water and at a height of h2 from the lower end of the tank, respectively, as shown in the figure. Water coming out from both the holes strike the ground at the same point. The ratio of h1 and h2 is
 A1B2C>1D<1
A1B2C>1D<1In a cylindrical water tank there are two small holes Q and P on the wall at a depth of h1 from the upper level of water and at a height of h2 from the lower end of the tank, respectively, as shown in the figure. Water coming out from both the holes strike the ground at the same point. The ratio of h1 and h2 is
 A1B2C>1D<1
A1B2C>1D<1A cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
AH/4BH/2C3H/4DH
A jet of water issunig from a hole mear the bottom of water tank is an…………………………. .
View SolutionA large tank having a small hole at the bottom is filled with water to a height h. If the stream of water coming out of the hole is directed vertically upwards it will :
View SolutionA water tank, open to the atmosphere, has a leak in it in the form of a circular hole, located at a height h below the open surface of water. The velocity of the water coming out of the hole is :
View SolutionA water tank, open to the atmosphere, has a leak in it in the form of a circular hole, located at a height h below the open surface of water. The velocity of the water coming out of the hole is :
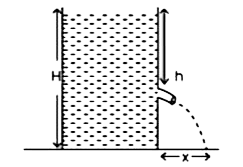
View SolutionThere is a hole h metre from its top of a tank filled with water. Calculate the distance x where the stream of water will touch the ground from the bottom (in m).
View Solution
