Two solid spherical balls of radii r1andr2(<r1) and of density σ are tied up with a long string and released in a viscous liquid column of lesser density ρ with the string just tatu as shown. The tension in the string when terminal velocity is attained is

43π(r42−r41r2−r1)(σ−ρ)g
23π(r32−r31)(ρ−σ)g
43(r32−r(1)3)(σ−ρ)g
43π(r42−r41r2+r1(σ−ρ)g
The correct Answer is:D
43π(r31+r32)(σ−ρ)g=6πη(r1+r2)v
and43πr32(σ−ρ)g=T+6πηr1v⇒T=43π(r42−r41)(σ−ρ)g(r1+r2)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - DISHA PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-1 CONCEPT BUILDER
59 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
- MOTION IN A PLANE BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -2 : CONCEPT APPLICATOR
28 Videos
Similar Questions
Two balls of same material of density ρ but radius r1 and r2 are joined by a light inextensible vertical thread and released from a large height in a medium of coefficient of viscosity =η. Find the terminal velocity acquired by the balls. Also find the tension in the string connecting both the balls when both of them are moving with terminal velocity. Neglect buoyancy and change in acceleration due to gravity.
View Solution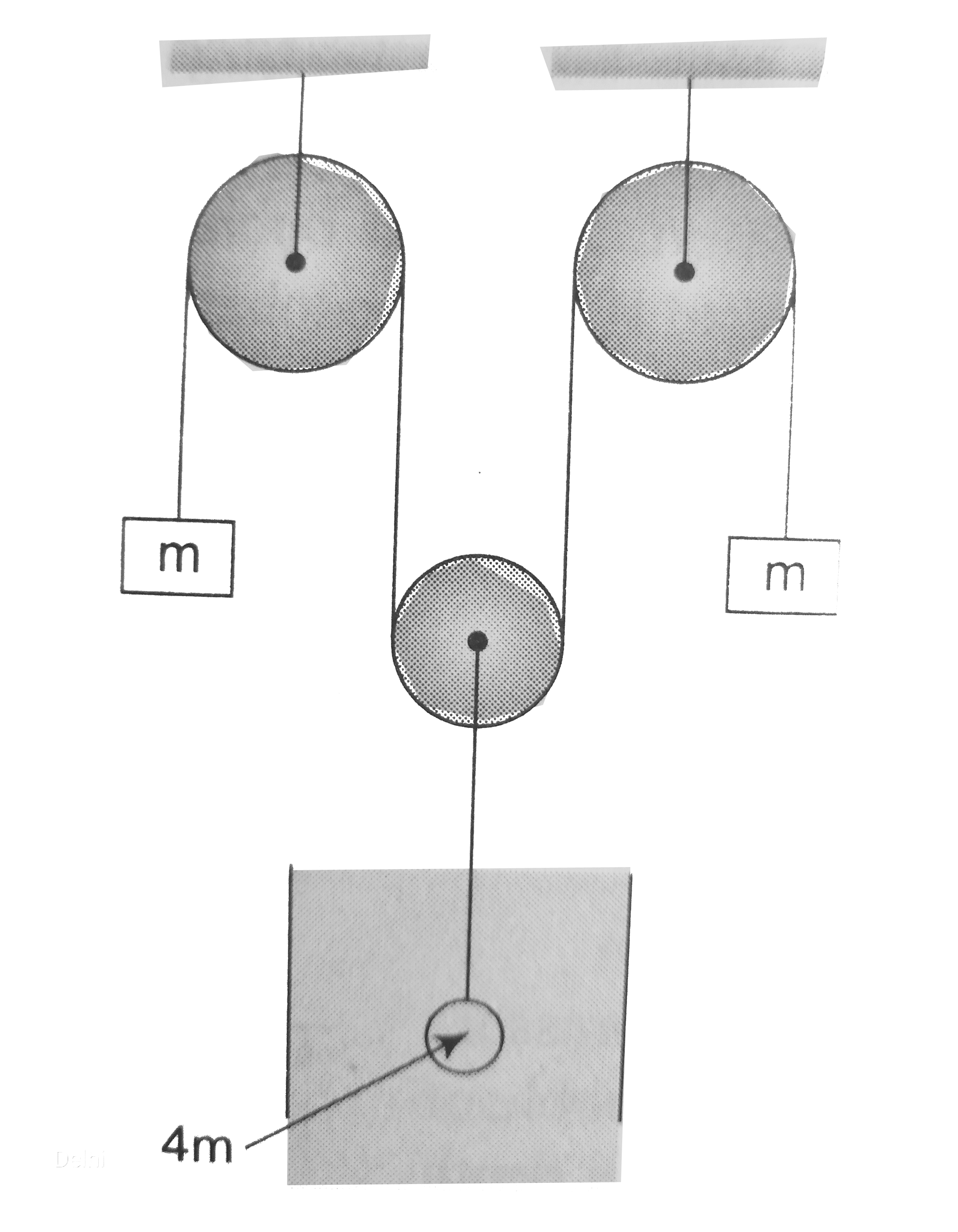
A spherical ball of mass 4m, density σ and radius r is attached to a pulley-mass system as shown in figure. The ball is released in a liquid of coefficient of viscosity η and density ρ(<σ2). If the length of the liquid column is sufficiently long, the terminal velocity attained by the ball is given by (assume all pulleys to be massless and string as massless and inextensible):
View Solution
Knowledge Check
A wooden block or mass m and density ρ is tied to a string, the other end of the string is fixed to bottom of a tank. The tank is filled with a liquid of density σ with σ>ρ. The tension in the string will be
A(σ−ρσ)mgB(σ−ρρ)mgCρmgσDσmgρTwo solid sphres of density ρ each and R and 2R are hung from a spring and a thread as shown if the thread is burnt.
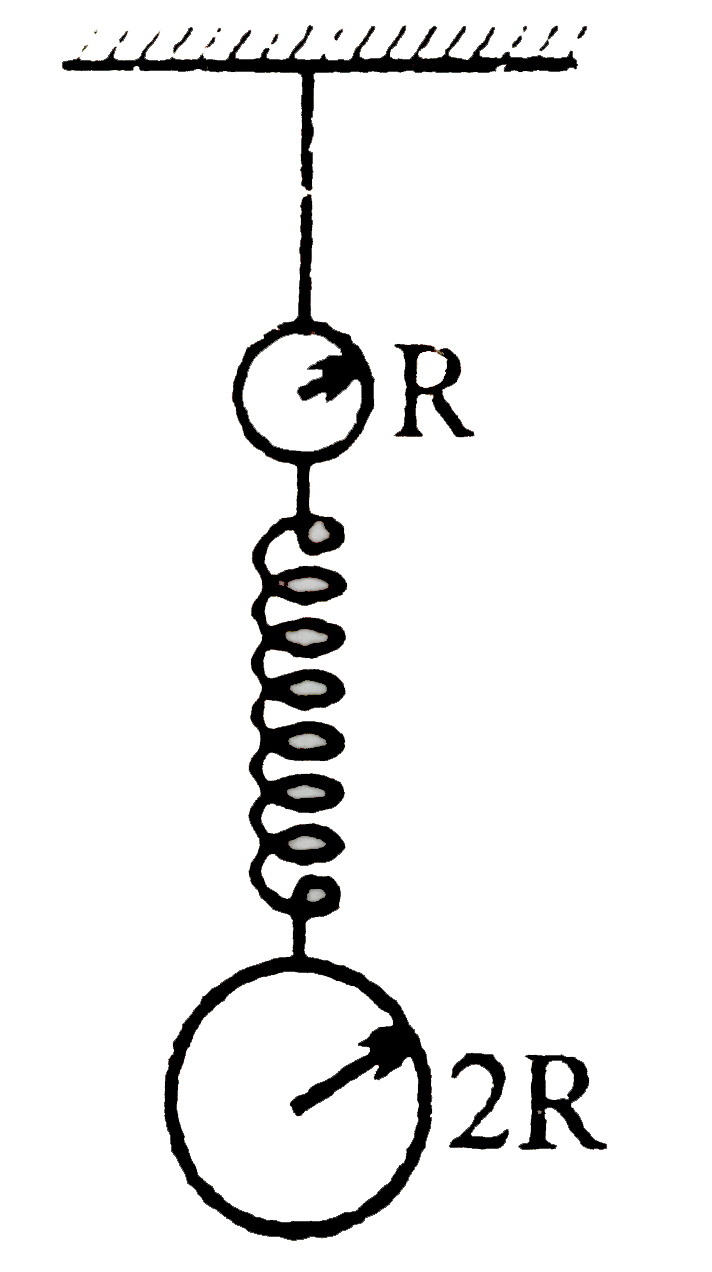 AThe initial acceleration of lower sphere is zeroBThe initial acceleration of upper sphere is 9g↓CThe initial acceleration of upper sphere is 3g↓DThe initial acceleration of lower sphere is g↓
AThe initial acceleration of lower sphere is zeroBThe initial acceleration of upper sphere is 9g↓CThe initial acceleration of upper sphere is 3g↓DThe initial acceleration of lower sphere is g↓
A spherical ball of mass 4m, density σ and radius r is attached to a pulley-mass system as shown in figure. The ball is released in a liquid of coefficient of viscosity η and density ρ(<σ2). If the length of the liquid column is sufficiently long, the terminal velocity attained by the ball is given by (assume all pulleys to be massless and string as massless and inextensible):A29r2(2σ−ρ)gηB29r2(σ−2ρ)gηC29r2(σ−4ρ)gηD29r2(σ−3ρ)gη
In the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
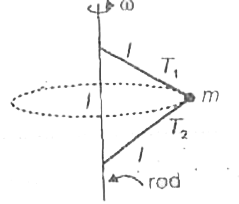
View SolutionIn the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when

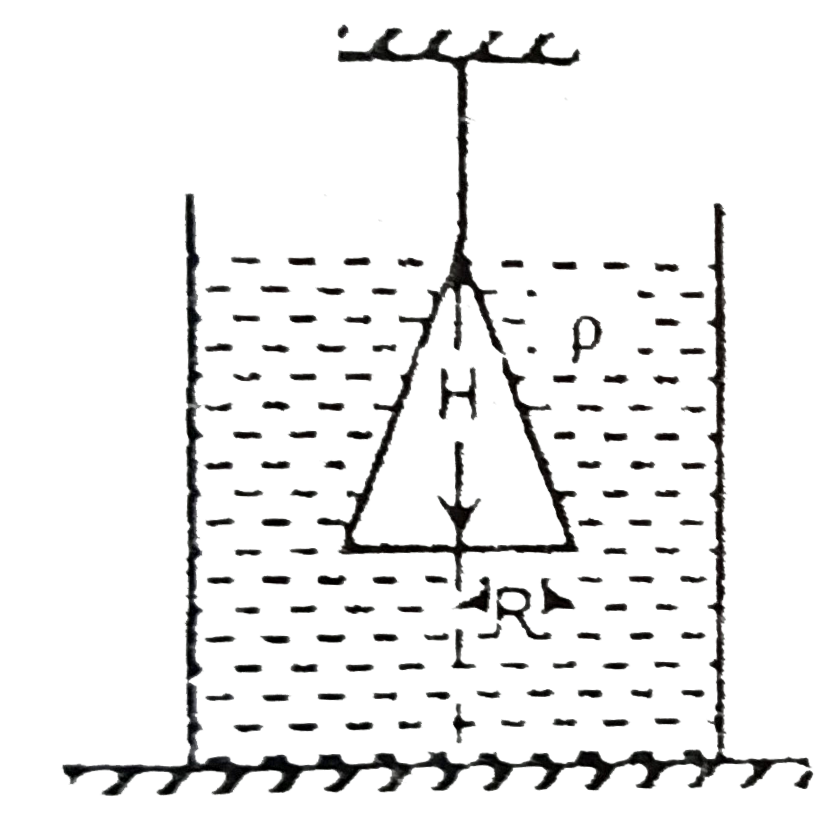
View SolutionA cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
View SolutionTwo planets have radii r1and2r1 and densities are ρ1and4ρ1 respectively. The ratio of their acceleration due to gravities is
View SolutionA cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is

View Solution
