A particle of mass m = 2 kg executes SHM in xy plane between points A and B under the action of force ¯¯¯F=Fxˆi+Fyˆj. Minimum time taken by the particle to move from A to B is 1 s. At t = 0 the particle is at x = 2 and y = 2. Then Fx as function of time t is

−4π2sinπt
−4π2cosπt
−6π2cosπt
None of these
The correct Answer is:B
Let the line joining AB represents axis .r.. By the conditions given .r. coordinate of the particle at time t is
ω=2πT=2π2=π r=2√2cosωt
x=rcos45∘,r√2=2cosπt
ax=−ω2x=−π22cosπt Fx=max=−4π2cosπt
Topper's Solved these Questions
- OSCILLATIONS BOOK - DISHA PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Exercise-1 : Concept Builder (TOPIC 3: Damped & Forced Oscillations and Resonance)
11 Videos
- NUCLEIBOOK - DISHA PUBLICATIONCHAPTER - NUCLEIEXERCISE - EXERCISE - 2 (CONCEPT APPLICATOR)
30 Videos
- PHYSICAL WORLD, UNITS AND MEASUREMENTSBOOK - DISHA PUBLICATIONCHAPTER - PHYSICAL WORLD, UNITS AND MEASUREMENTSEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
Similar Questions
A particle of mass m=2kg executes SHM in xy- plane between point A and B under action of force →F=Fxˆi+Fyˆj. Minimum time taken by particle to move from A to B is 1 sec. At t=0 the particle is at x=2 and y=2. Then Fx as function of time t is
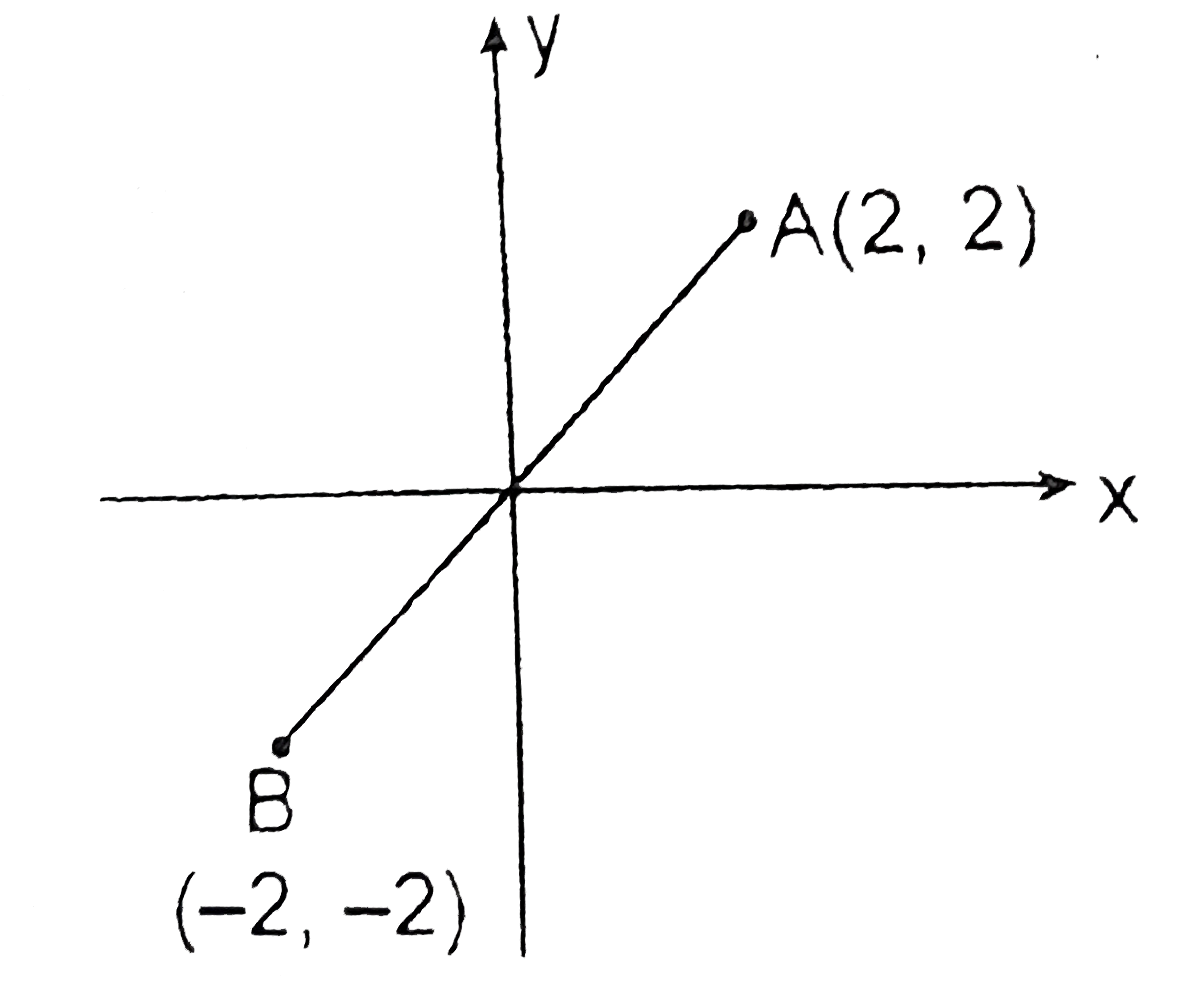
View SolutionA particle of mass m=2kg executes SHM in xy- plane between point A and B under action of force →F=Fxˆi+Fyˆj. Minimum time taken by particle to move from A to B is 1 sec. At t=0 the particle is at x=2 and y=2. Then Fx as function of time t is

View Solution
Knowledge Check
A particle of mass m=2kg executes SHM in xy- plane between point A and B under action of force →F=Fxˆi+Fyˆj. Minimum time taken by particle to move from A to B is 1 sec. At t=0 the particle is at x=2 and y=2. Then Fx as function of time t is
 A−4π2sinπtB−4π2cosπtC4π2cosπtDNone of these
A−4π2sinπtB−4π2cosπtC4π2cosπtDNone of theseA particle of mass 2kg moves in the xy plane under the action of a constant force →F where →F=ˆi−ˆj. Initially the velocity of the particle is 2ˆj. The velocity of the particle at time t is
A12(t+4)ˆi−12tˆjBt(ˆi−ˆj)C12t(ˆi−ˆj)D12tˆi+12(t+4)ˆjParticle moves from point A to point B along the line shown in figure under the action of force. evcF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
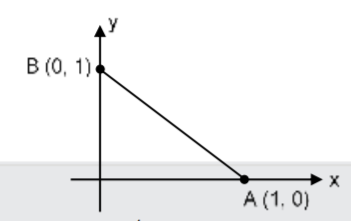 A1 JB1/2 JC2 JD3 J
A1 JB1/2 JC2 JD3 J
A particle of mass 2kg moves in the xy plane under the action of a constant force →F where →F=ˆi−ˆj. Initially the velocity of the particle is 2ˆj. The velocity of the particle at time t is
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. evcF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.

View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. VecF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.

View SolutionA particle of mass 2 kg starts motion at time t = 0 under the action of variable force F = 4t (where F is in N and t is in s). The work done by this force in first two second is
View SolutionA particle of mass 2 kg starts motion at time t = 0 under the action of variable force F = 4t (where F is in N and t is in s). The work done by this force in first two second is
View Solution
