A uniform pole of length l = 2 L is laid on smooth horizontal table as shown in figure. The mass of pole is M and it is connected to a frictionless axis at O.A spring with force constant k is connected to the other end. The pole is displaced by a small angle θ0 from equilibrium position and released such that it performs small oscillations. Then

ω0=√M3k
ω0=√k3M
ω0=√3kM
ω0=√k2M
The correct Answer is:C
I=13M(2L)2=43ML2
Force applied by the spring is F=−kξmpliesF=−k(2Lθ) (θ is the angular displacement from the equilibrium position). Further
τ=∣∣→l×→F∣∣=4L2ksinθ=−4L2kθ
Also, τ=Iα=−4L2kθ
⇒θ+3kMθ=0⇒ω0=√3kM
Topper's Solved these Questions
- OSCILLATIONS BOOK - DISHA PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Exercise-1 : Concept Builder (TOPIC 3: Damped & Forced Oscillations and Resonance)
11 Videos
- NUCLEIBOOK - DISHA PUBLICATIONCHAPTER - NUCLEIEXERCISE - EXERCISE - 2 (CONCEPT APPLICATOR)
30 Videos
- PHYSICAL WORLD, UNITS AND MEASUREMENTSBOOK - DISHA PUBLICATIONCHAPTER - PHYSICAL WORLD, UNITS AND MEASUREMENTSEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
Similar Questions

A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
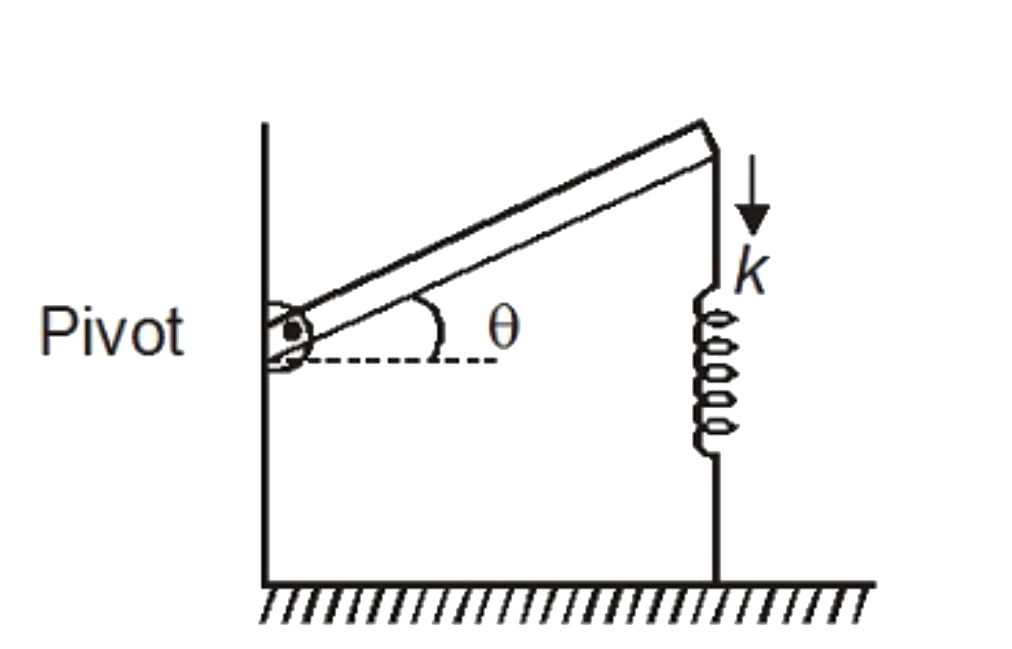
View Solution
Knowledge Check

A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion isA√3kmB√k3mC√3km+3g2LD√kmA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
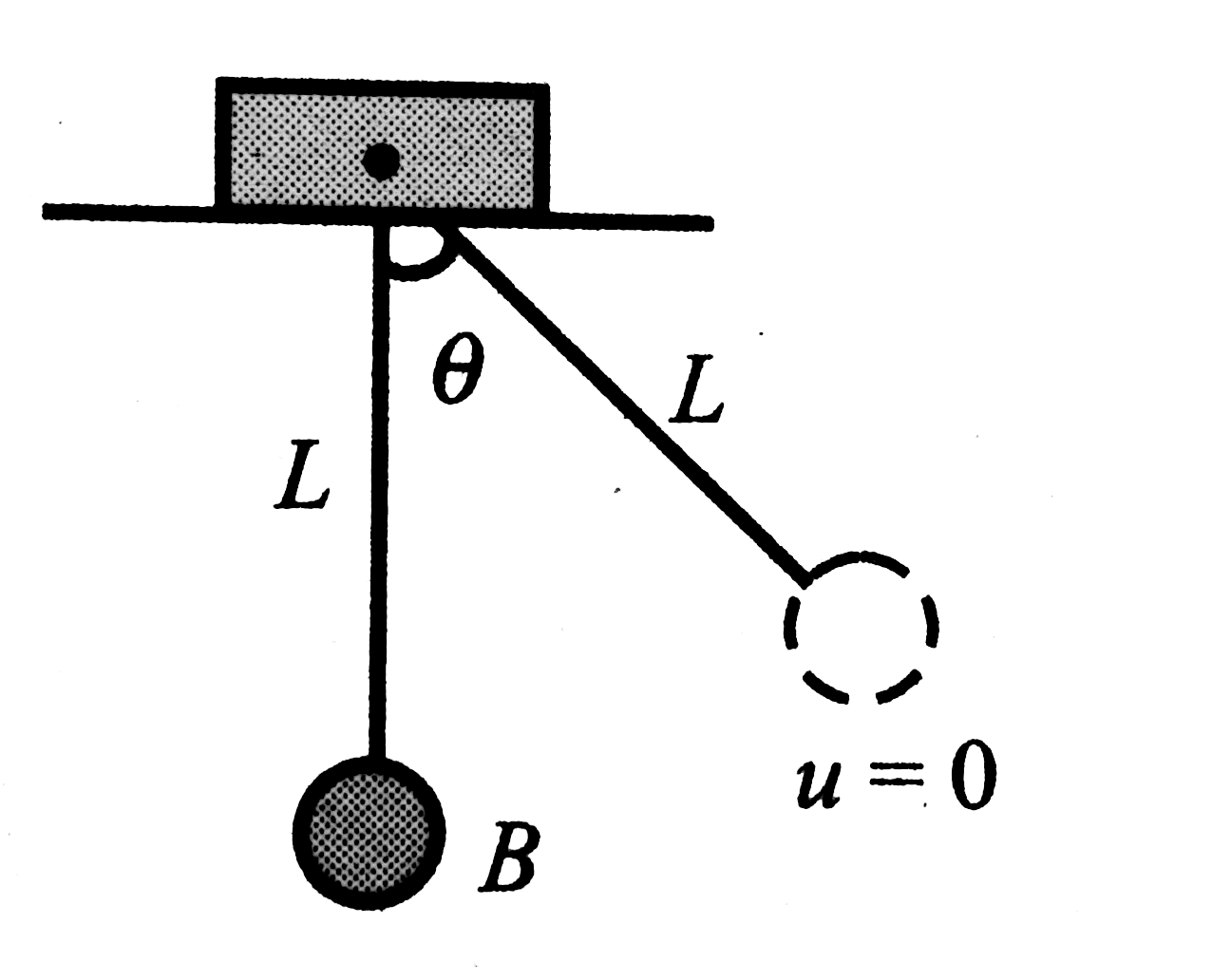
Tension in string when it is vertical, isAmgBmg(2−cosθ)Cmg(3−2cosθ)Dnone of these
A horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is

View SolutionA long uniform rod of length L and mass M is free to rotate in a horizontal plane about a vertical axis through its one end 'O'. A spring of force constant k is connected between one end of the rod and PQ. When the rod is in equilibrium it is parallel to PQ.

(a)What is the period of small oscillation that result when the rod is rotated slightly and released ?
(b) What will be the maximum speed of the displacement end of the rod, if the amplitude of motion is θ0?
View SolutionA long uniform rod of length L and mass M is free to rotate in a horizontal plane about a vertical axis through its one end 'O'. A spring of force constant k is connected between one end of the rod and PQ. When the rod is in equilibrium it is parallel to PQ.

(a)What is the period of small oscillation that result when the rod is rotated slightly and released ?
(b) What will be the maximum speed of the displacement end of the rod, if the amplitude of motion is θ0?
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.

Tension in string when it is vertical, is
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View Solution
