A long wire is bent into shape ABCDE as shown in fig., with BCD being a semicircle with centre O and radius r metre. A current of I amp. Flows through it in the direction A→B→C→D→E . Then the magnetic induction at the point O of the figure in vacuum is

μ0[I2πr+I4r]
μ0[I2πr−I4r]
μ0I/4r
μ0I/πr
The correct Answer is:A
B=μ04π[Ir+πIr+Ir]=μ04π[2Ir+πIr]
=μ0[I2πr+I4r]
(The direction of →B is into the page.)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - DISHA PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXERCISE - 1 : Concept Builder (Topic wise) (Topic 3 : Force and torque on current carrying conductor and moving coil Galvanometor )
14 Videos
- MOTION IN A STRAIGHT LINEBOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-2
30 Videos
- NUCLEIBOOK - DISHA PUBLICATIONCHAPTER - NUCLEIEXERCISE - EXERCISE - 2 (CONCEPT APPLICATOR)
30 Videos
Similar Questions
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View SolutionA wire is bent in the form of a circular arc of radius r with a straight portion AB. If the current in the wire is i, then the magnetic induction at point O is

View Solution
Knowledge Check
A long current wire is bent in the shapes shown in figure. The circular portion has radius R. The magnetic induction at the center of the circular segment is
 A−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]Bμ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]C−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]Dμ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]
A−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]Bμ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]C−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]Dμ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2An infinitely long straight conduction is bent into the shape as shown in the figure . It carries a current of I ampere and the radius of the circular loop is r metre. Then the magnetic induction at its centre will be
 Aμ04π2ir(π+1)Bμ04π2ir(π−1)CzeroDInfinite
Aμ04π2ir(π+1)Bμ04π2ir(π−1)CzeroDInfinite
A wire is bent in the form of a circular arc of radius r with a straight portion AB. If the current in the wire is i, then the magnetic induction at point O is

View SolutionTwo inflinitely long wires carrying current I, are bent as shown in the figure. Find the magnetic induction at point C.
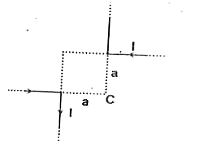
View SolutionA current of I ampere is flowing through each of the bent wires as shown the magnitude and direction of magnetic field at O is
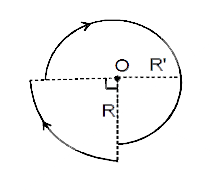
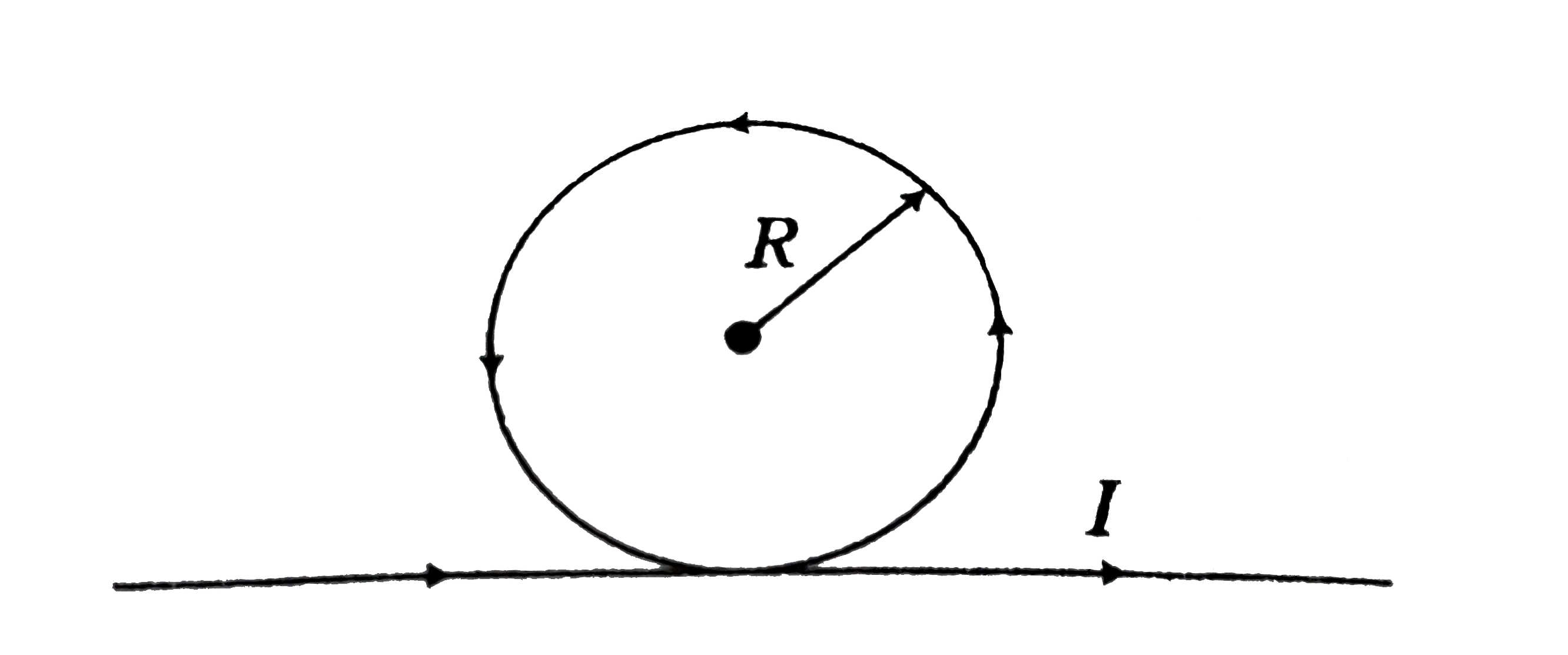
View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is
View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View Solution
