An otherwise infiniye, straight wire has two concentric loops of radii a and b carrying equal current in opposite directions as shown in Fig. The magnetic field at the common center is zero for

ab=π−1π
ab=−ππ+1
ab=π−1π+1
ab=π+1π−1
The correct Answer is:B
Bcentre=0
μ0I4πb⊙+μ0I4πb⊙+μ0I2b⊙+μ0I2a⊗=0
⇒μ0I4πb+μ0I2b−μ0I2a=0⇒12πb+12b=12a
⇒ab=πpr+1
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - DISHA PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXERCISE - 1 : Concept Builder (Topic wise) (Topic 3 : Force and torque on current carrying conductor and moving coil Galvanometor )
14 Videos
- MOTION IN A STRAIGHT LINEBOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-2
30 Videos
- NUCLEIBOOK - DISHA PUBLICATIONCHAPTER - NUCLEIEXERCISE - EXERCISE - 2 (CONCEPT APPLICATOR)
30 Videos
Similar Questions
An otherwise infinite, straight wire has two concentric loops of radii a and b carrying equal currents in opposite directions as shown in Fig. The magnetic field at the common centre is zero for
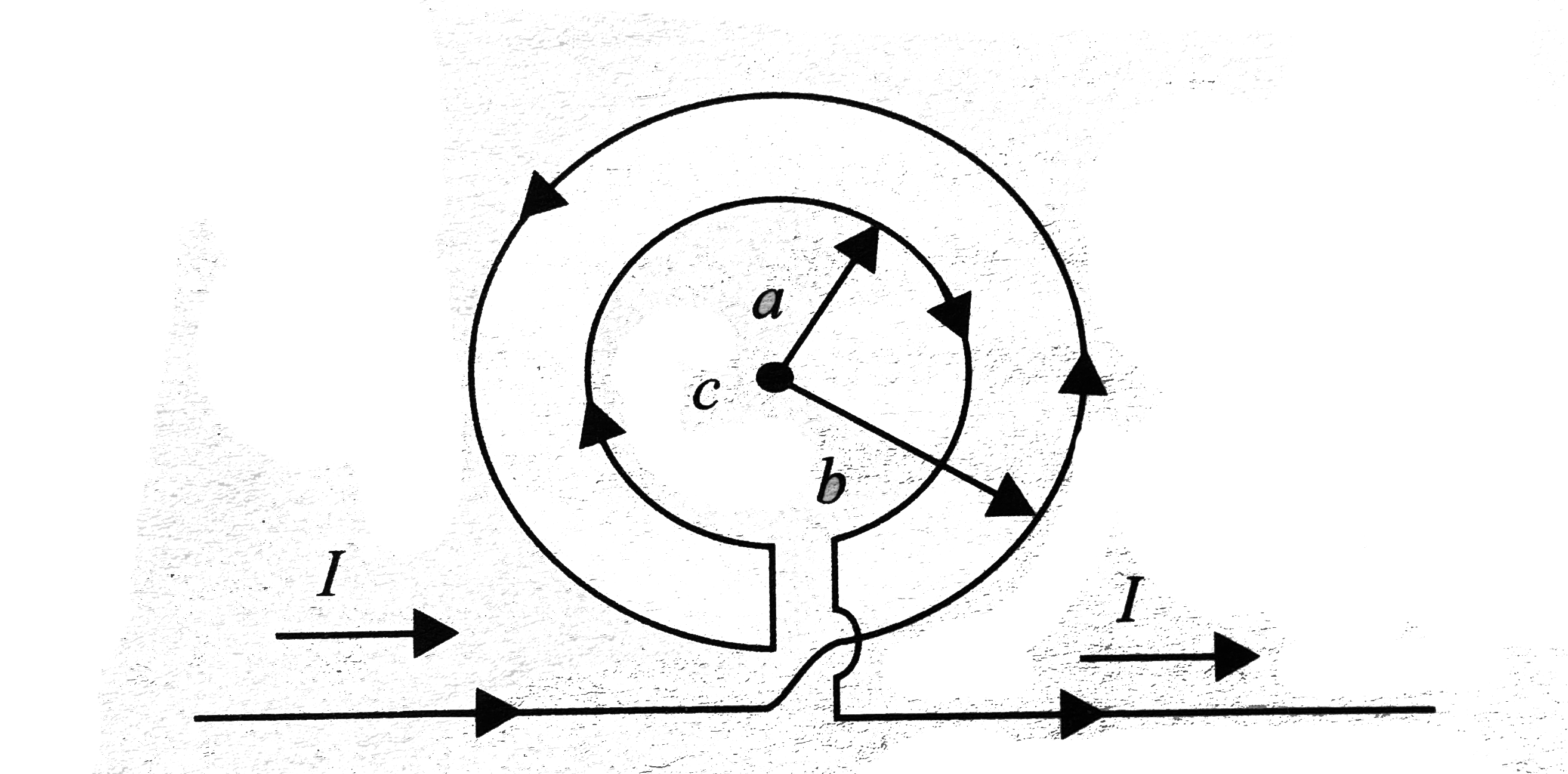
View SolutionIn a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero.
View Solution
Knowledge Check
An otherwise infinite, straight wire has two concentric loops of radii a and b carrying equal currents in opposite directions as shown in Fig. The magnetic field at the common centre is zero for
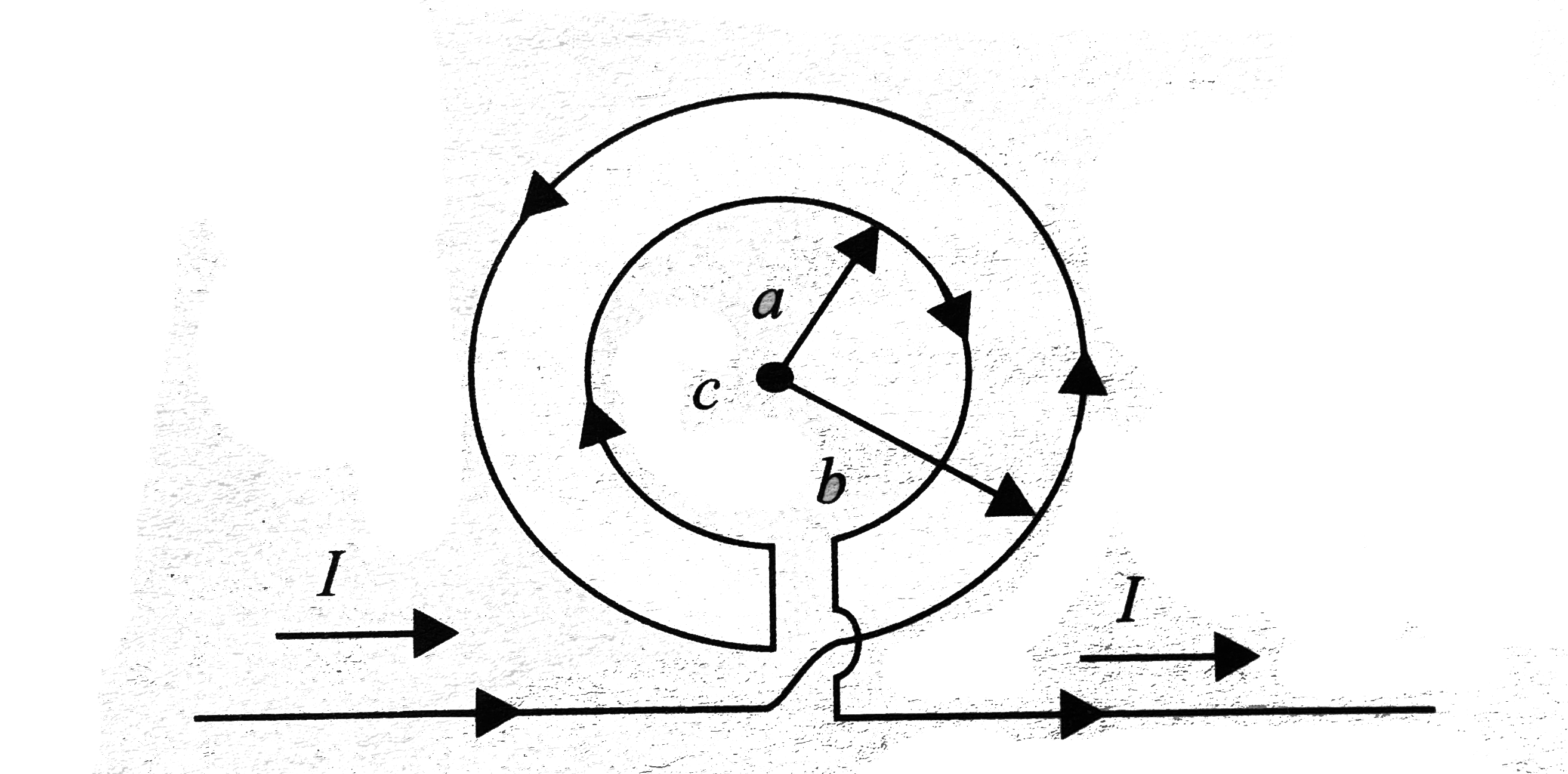 Aab=π−1πBab=ππ+1Cab=π−1π+1Dab=π+1π−1
Aab=π−1πBab=ππ+1Cab=π−1π+1Dab=π+1π−1In a coaxial, straght cable, the central conductor and the outer conductor carry equal currents in opposite directions.The magnetic field is non-zero.
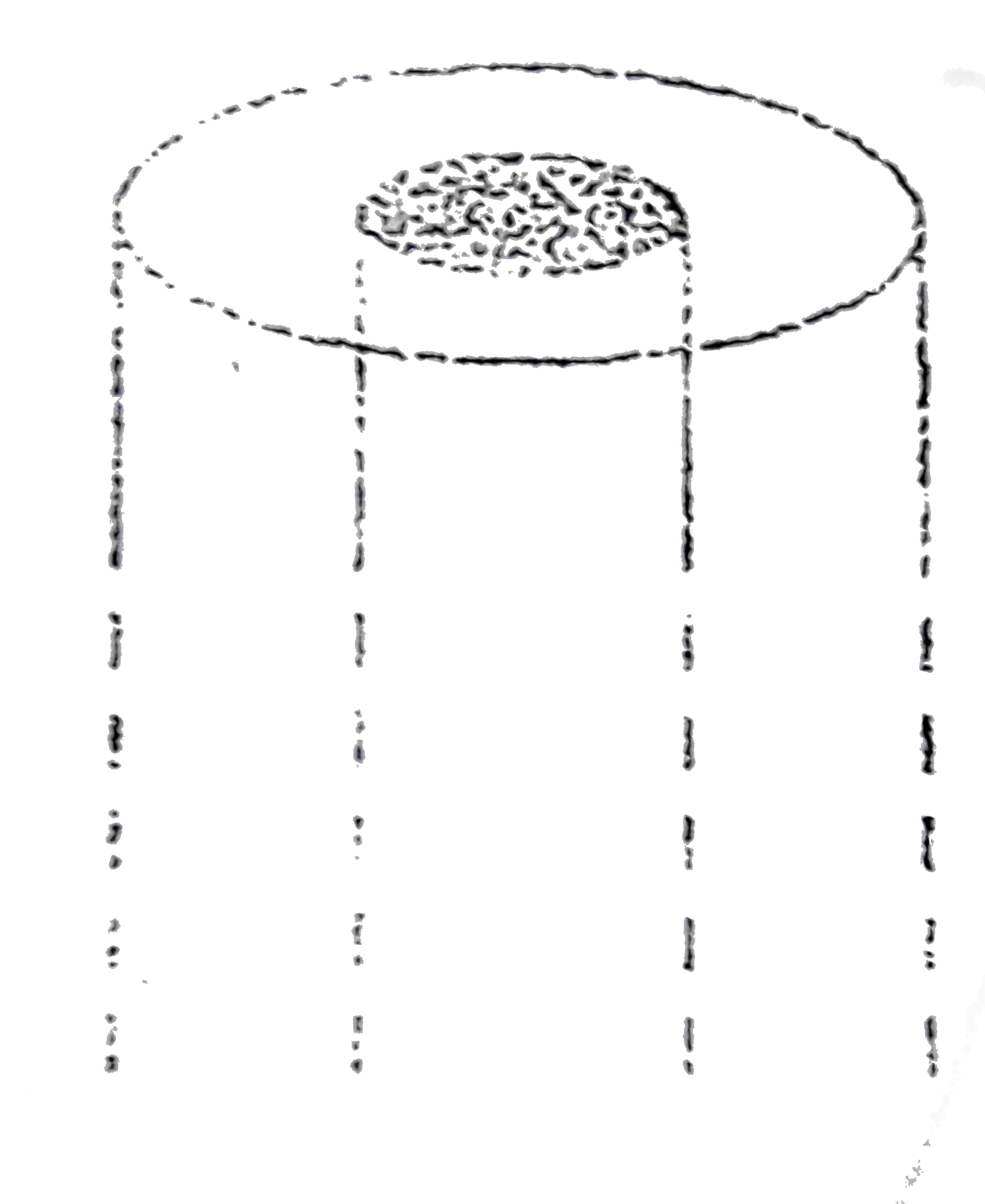 Aoutside the cableBinside the inner conductor except axis of the conductorCall the point inside the outer conductor and outside inner conductorDonly on axis of conductors
Aoutside the cableBinside the inner conductor except axis of the conductorCall the point inside the outer conductor and outside inner conductorDonly on axis of conductorsThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
 AzeroBμ0I4(1R1−1R2)Cμ0I4(1R2+1R1)Dμ0I2(1R1−1R2)
AzeroBμ0I4(1R1−1R2)Cμ0I4(1R2+1R1)Dμ0I2(1R1−1R2)
In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero.
View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,

View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionInfinite number of straight wires each carrying current I are equally placed as shown in the figure Adjacent wires have current in opposite direction Net magnetic field at point P is
 .
.
View Solution
