The magnetic field at O due to current in the infinite wire forming a loop as shown in Fig. is

A
μ0I2πd(cosϕ1+cosϕ2)
B
μ0I4π2Id(tanθ1+tanθ2)
C
μ0I4πR(sinϕ1+sinϕ2)
D
μ0I4πR(cosθ1+sinθ2)
Text Solution
The correct Answer is:A
Using B=μ0I4πd[sinθ1+sinθ2]
But θ1+ϕ1=90∘ or θ1=90∘−ϕ
sinθ1=sin(90∘−ϕ1)=cosθ1
Similarly , sinθ2=cosϕ2
Bnet=μ0I2πd(cosθ1+cosϕ2)
|
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - DISHA PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXERCISE - 1 : Concept Builder (Topic wise) (Topic 3 : Force and torque on current carrying conductor and moving coil Galvanometor )
14 Videos
- MOTION IN A STRAIGHT LINEBOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-2
30 Videos
- NUCLEIBOOK - DISHA PUBLICATIONCHAPTER - NUCLEIEXERCISE - EXERCISE - 2 (CONCEPT APPLICATOR)
30 Videos
Similar Questions
Knowledge Check
The magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.
 Aμ0I2πd(cosϕ1+cosϕ2)Bμ04π2Id(tanθ1+tanθ2)Cμ04πId(sinϕ1+sinϕ2)Dμ04πId(cosθ1+cosθ2)
Aμ0I2πd(cosϕ1+cosϕ2)Bμ04π2Id(tanθ1+tanθ2)Cμ04πId(sinϕ1+sinϕ2)Dμ04πId(cosθ1+cosθ2)Magnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
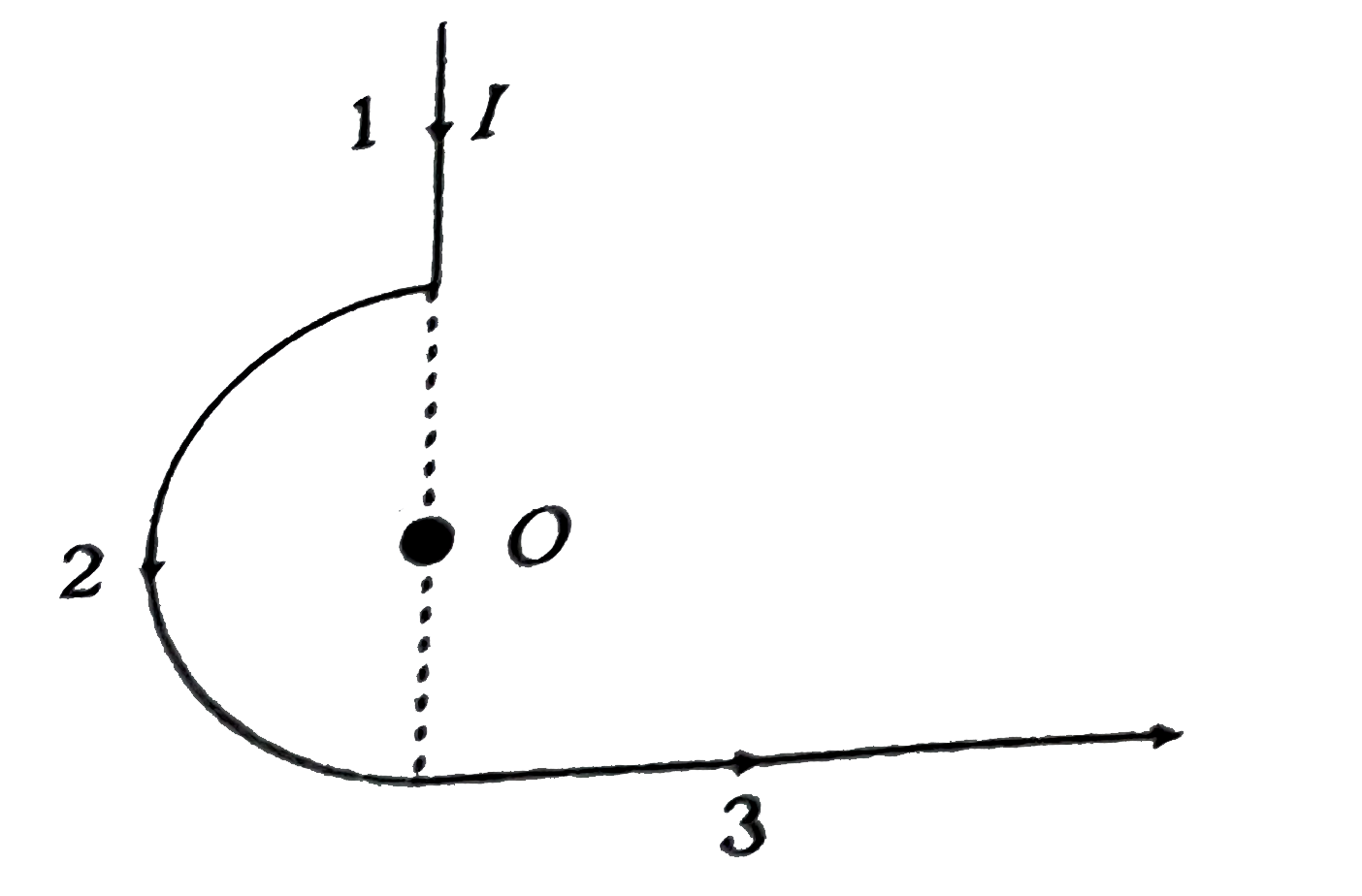 Aμ0I4πRBμ0I4R−μ0I4πRCμ0I4R−μ0I2πRDμ0I4R+μ0I4πR
Aμ0I4πRBμ0I4R−μ0I4πRCμ0I4R−μ0I2πRDμ0I4R+μ0I4πRThe magnetic field at the centre of the circular loop as shown in Fig. when a single wire is bent to form a circular loop and also extends to form straight sections is
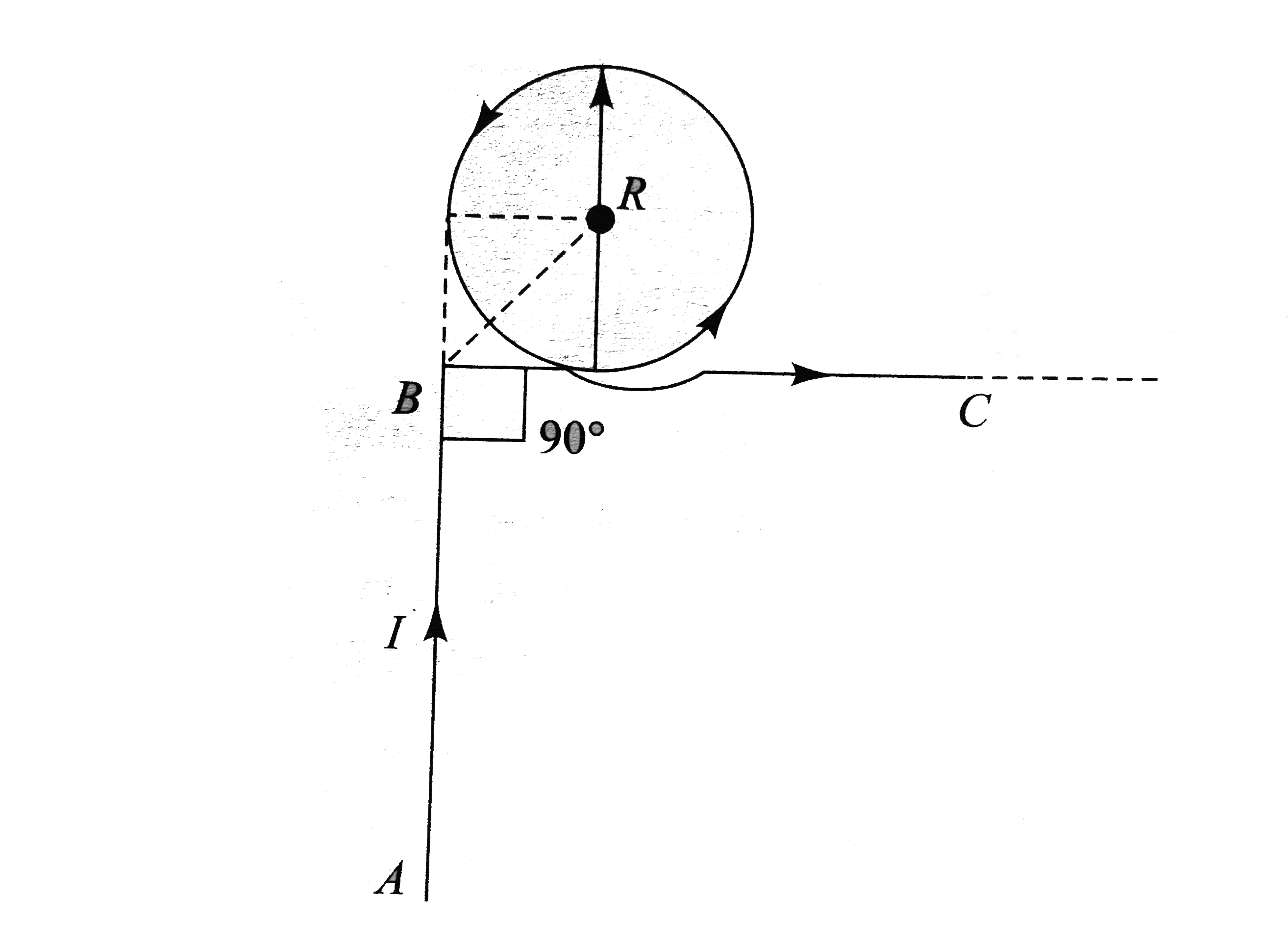 Aμ0I2R⊙Bμ0I2R(1+1π√2)⊙Cμ0I2R(1−1π√2)⊗Dμ0IR(1−1π√2)⊗
Aμ0I2R⊙Bμ0I2R(1+1π√2)⊙Cμ0I2R(1−1π√2)⊗Dμ0IR(1−1π√2)⊗
The magnetic field at the centre of the circular loop as shown in Fig. when a single wire is bent to form a circular loop and also extends to form straight sections is
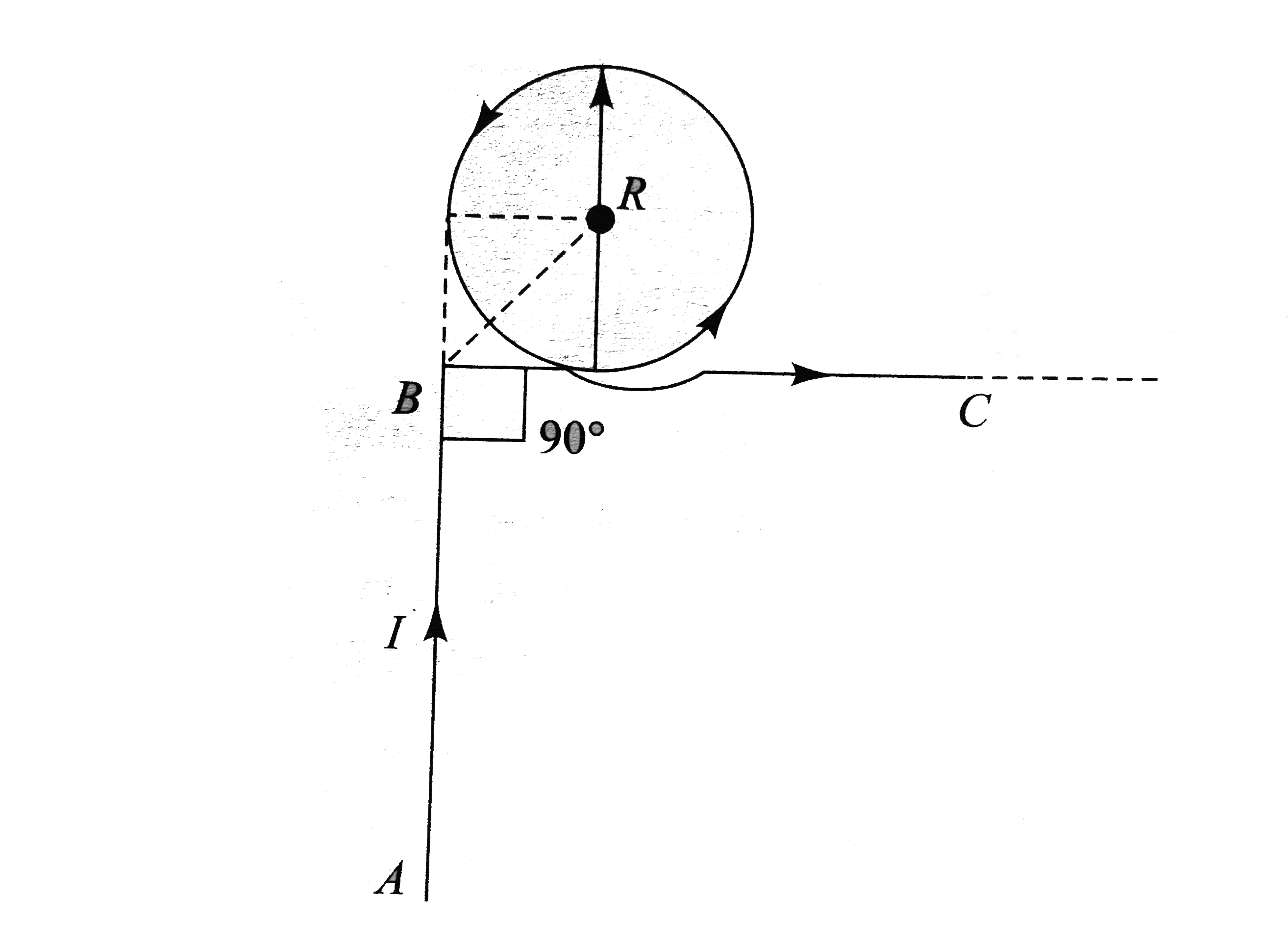
View SolutionThe magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :
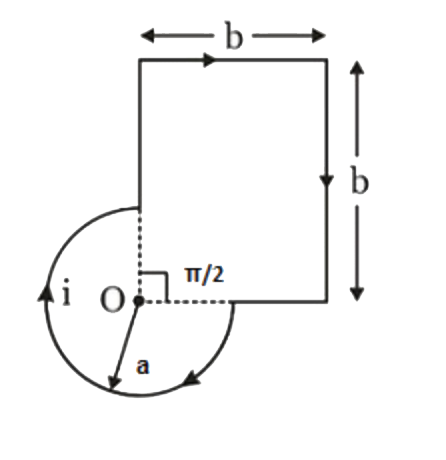
View SolutionFind magnetic field at O due to the current carrying conductor as shown in the figure.
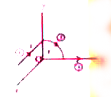
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure. Given r1>r2
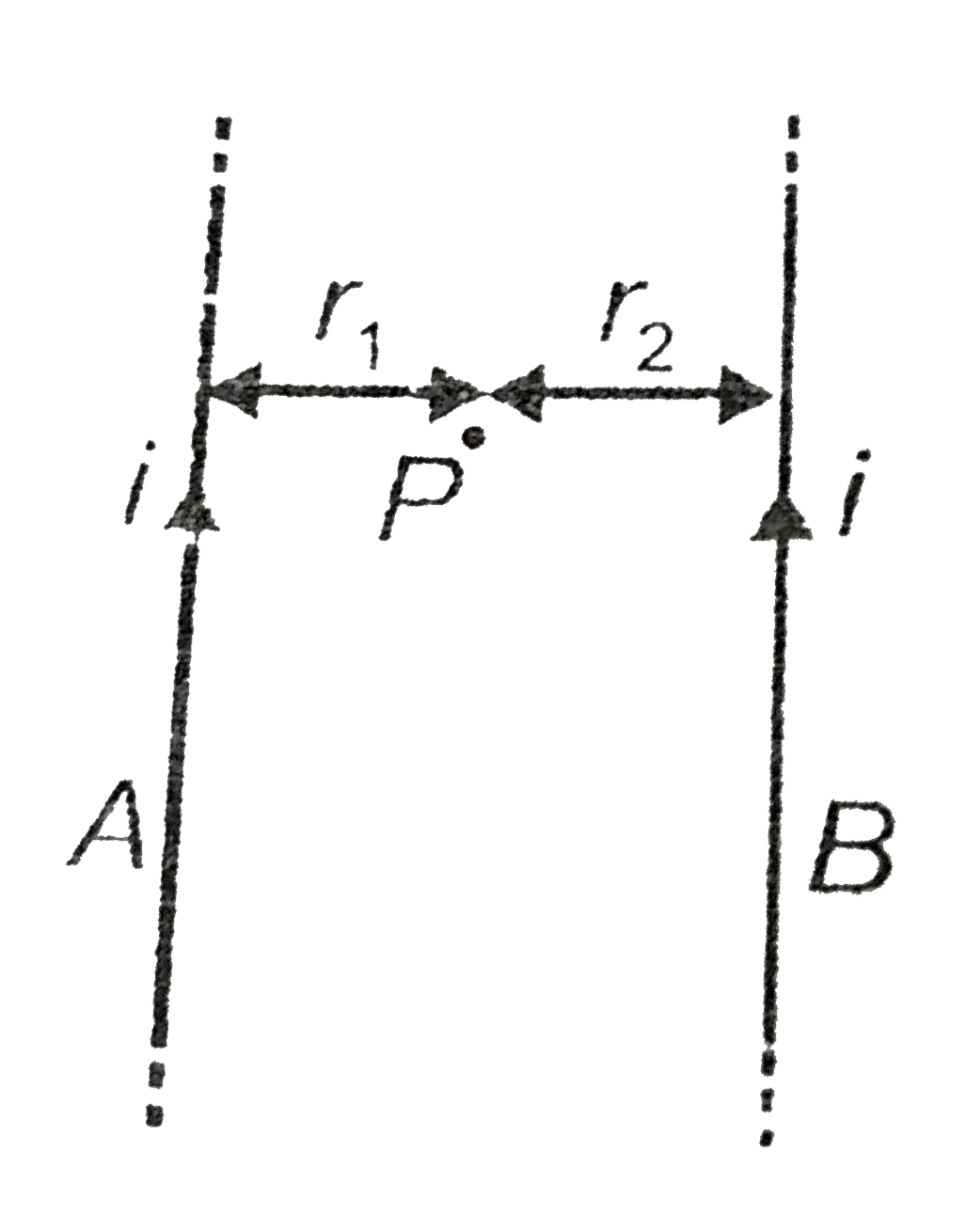
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure. Given r1>r2

View Solution
