एक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ADC=∠BAC है। दर्शाएँ कि CA2=CB⋅CD है।
Step by step video & image solution for एक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि angleADC=angleBAC है। दर्शाएँ कि CA^(2)=CB*CD है। by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज BOOK - ALOK BHARTI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - दीर्घ उत्तरीय प्रश्न एवं उत्तर
3 Videos
- त्रिभुज BOOK - ALOK BHARTI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - दीर्घ उत्तरीय प्रश्न एवं उत्तर
3 Videos
- त्रिकोणमितीय अनुपात BOOK - ALOK BHARTI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात EXERCISE - प्रश्नावली 8.6
8 Videos
- दो चरों में रैखिक समीकरण BOOK - ALOK BHARTI PUBLICATIONCHAPTER - दो चरों में रैखिक समीकरण EXERCISE - प्रश्नावली 3.5
38 Videos
Similar Questions
सिद्ध करें कि यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओं को काटते हुए कोई रेखा खींचे तो यह त्रिभुज की अन्य दोनों भुजाओं की समान अनुपात में विभाजित करती है।
View Solutionसिद्ध करें कि यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओं को काटते हुए कोई रेखा खींचे तो यह त्रिभुज की अन्य दोनों भुजाओं की समान अनुपात में विभाजित करती है।
View Solution200 मीटर ऊँची एक पहाड़ी की चोटी से एक खंभे के शीर्ष एवं आधार के अवनमन कोण क्रमश : 30∘ एवं 60∘ है। खंभे की ऊँचाई तथा मीनार से उसकी दुरी ज्ञात करे
View Solutionदो संख्याओं का योगफल 15 है। यदि उनके व्युत्क्रम का योगफल हो 310तो वह संख्या ज्ञात करें।
View Solutionएक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ADC=∠BAC है । दर्शाइए कि CA2=CB⋅CD है ।
View Solutionचित्र 1 में त्रिभुज ABC की भुजा BC पर बिन्दु D इस प्रकार है कि ∠ADC=∠BAC, तो सिद्ध कीजिए CACD=CBCA
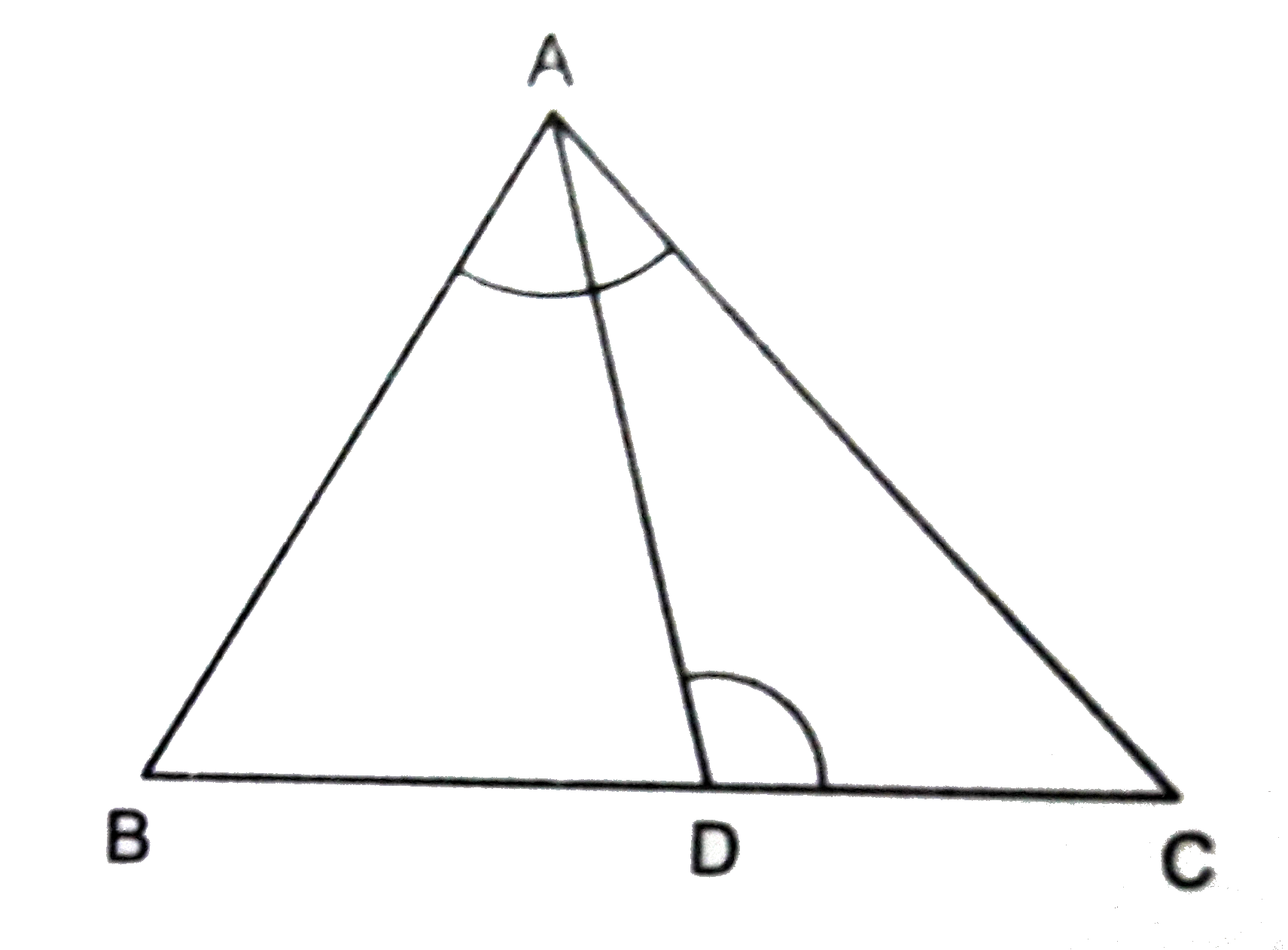
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
View SolutionD is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC . Show that CA2 = CB. CD.
View SolutionIn △ABC, D is a point on side BC such that ∠ADC=∠BAC. If CA = 12 cm, CB = 8 cm, then CD is equal to:
त्रिभुज ABC में भुजा BC पर D बिंदु इस प्रकार स्थित है कि ∠ADC=∠BAC होता है। यदि CA = 12 सेमी, CB = 8 सेमी, तो CD निम्नलिखित में किसके बराबर है?
View SolutionThe area of a triangle ABC is one unit. DE is a straight line parallel to BC , joining the points D and E on AB and AC respectively such that AD : DB = 1 : 6. The ratio of the areas of the triangles ADE and ABC is : एक त्रिभुज ABC का क्षेत्रफल 1 इकाई है | DE, BC के समानांतर एक सीधी रेखा है जो क्रमशः AB और AC पर स्थित बिंदु D तथा E को इस प्रकार जोड़ती है कि AD : DB = 1 : 6 है | त्रिभुज ADE और ABC के क्षेत्रफल में अनुपात ज्ञात करें |
View Solution
